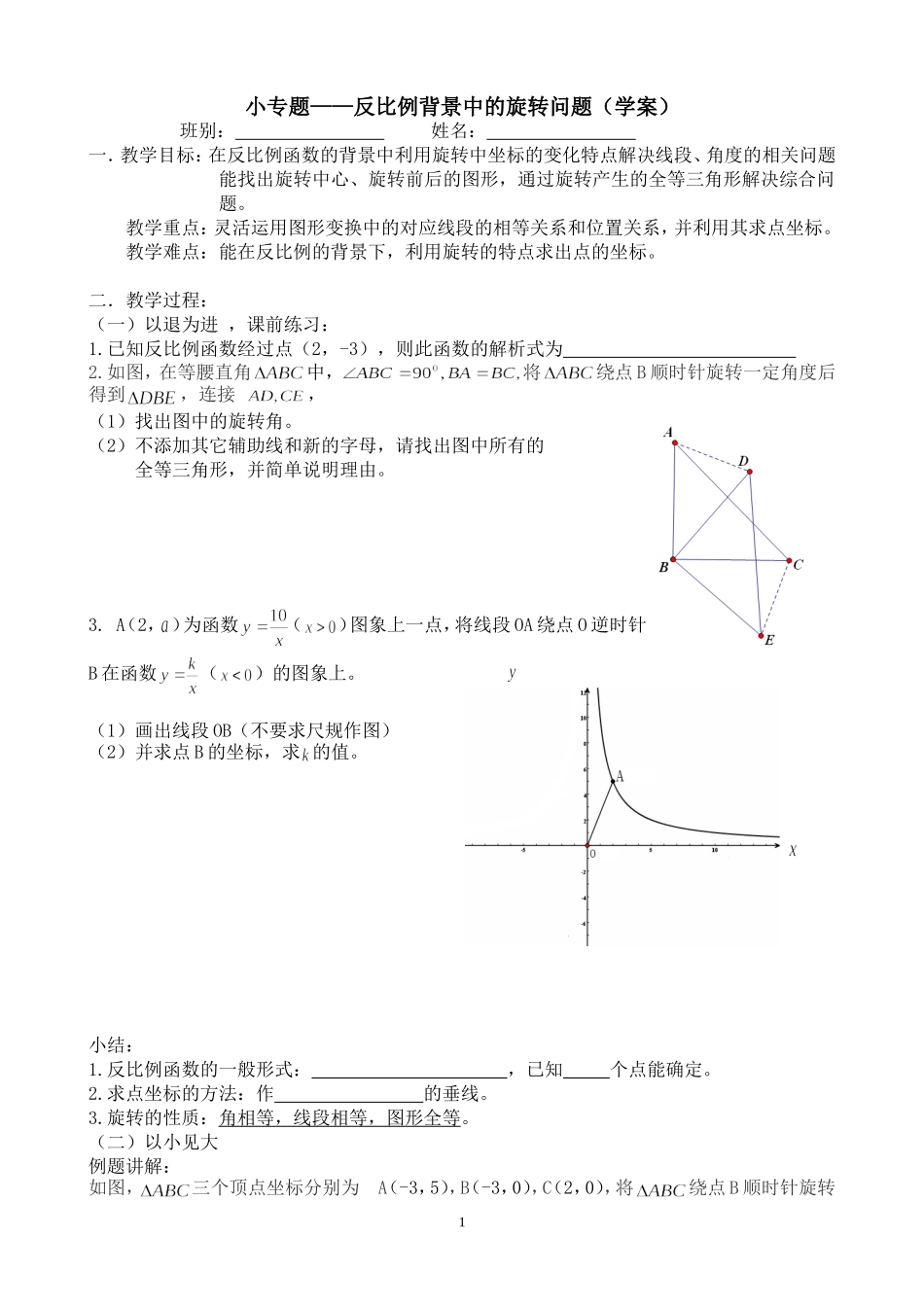
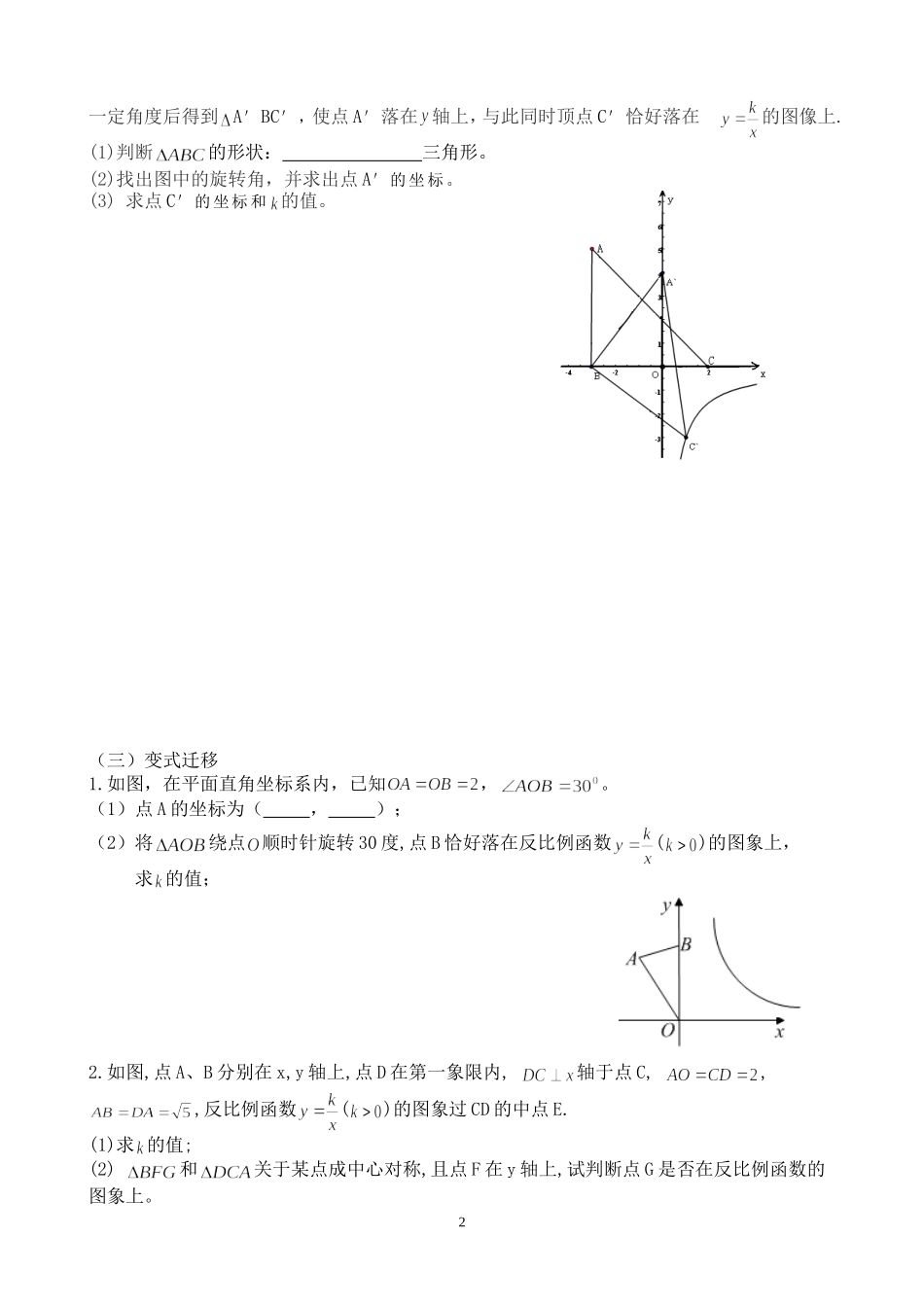
小专题——反比例背景中的旋转问题(学案)班别:姓名:一.教学目标:在反比例函数的背景中利用旋转中坐标的变化特点解决线段、角度的相关问题能找出旋转中心、旋转前后的图形,通过旋转产生的全等三角形解决综合问题。教学重点:灵活运用图形变换中的对应线段的相等关系和位置关系,并利用其求点坐标。教学难点:能在反比例的背景下,利用旋转的特点求出点的坐标。二.教学过程:(一)以退为进,课前练习:1.已知反比例函数经过点(2,-3),则此函数的解析式为2.如图,在等腰直角中,将绕点B顺时针旋转一定角度后得到,连接,(1)找出图中的旋转角。(2)不添加其它辅助线和新的字母,请找出图中所有的全等三角形,并简单说明理由。3.A(2,)为函数()图象上一点,将线段OA绕点O逆时针旋转得到线段OB,点B在函数()的图象上。(1)画出线段OB(不要求尺规作图)(2)并求点B的坐标,求的值。小结:1.反比例函数的一般形式:,已知个点能确定。2.求点坐标的方法:作的垂线。3.旋转的性质:角相等,线段相等,图形全等。(二)以小见大例题讲解:如图,三个顶点坐标分别为A(-3,5),B(-3,0),C(2,0),将绕点B顺时针旋转1一定角度后得到A'BC',使点A'落在轴上,与此同时顶点C'恰好落在的图像上.(1)判断的形状:三角形。(2)找出图中的旋转角,并求出点A'的坐标。(3)求点C'的坐标和的值。(三)变式迁移1.如图,在平面直角坐标系内,已知,。(1)点A的坐标为(_____,_____);(2)将绕点顺时针旋转30度,点B恰好落在反比例函数()的图象上,求的值;2.如图,点A、B分别在x,y轴上,点D在第一象限内,轴于点C,,,反比例函数()的图象过CD的中点E.(1)求的值;(2)和关于某点成中心对称,且点F在y轴上,试判断点G是否在反比例函数的图象上。2(3)在(2)的条件下,画出对称中心M,并求对称中心的坐标。四、课堂小结1.利用待定系数法求反比例函数的步骤。2.在反比例函数的背景下,分析旋转前后的图形特点,求旋转后点的坐标。(1)找到旋转前后相等的线段,相等的角,全等三角形。(2)在坐标系中,学会经过点作垂线的方法,利用勾股定理求线段长度。(3)熟练掌握点坐标和长度间的相互转化。五、能力训练如图,在平面直角坐标系中,,轴于点C,点A在反比例函数的图象上。(1)求反比例函数的表达式。(2)若将绕点B按逆时针方向旋转600得到,求出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由。34