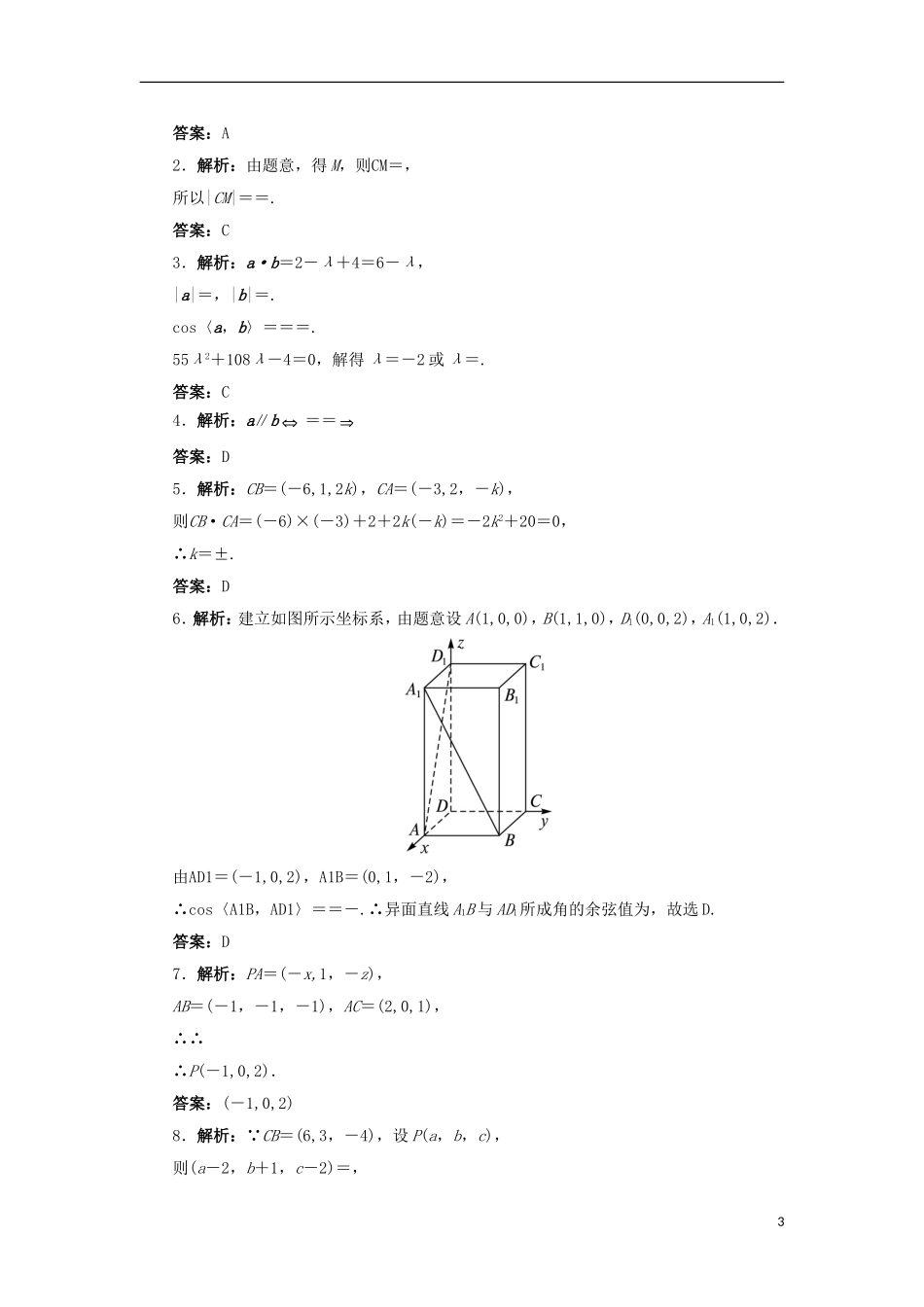
3.1.4空间向量的直角坐标运算自我小测1.已知A(3,4,5),B(0,2,1),O(0,0,0),若OC=AB,则C的坐标是()A.B.C.D.2.已知A(3,3,1),B(1,0,5),C(0,1,0),则AB的中点M到点C的距离|CM|=()A.B.C.D.3.若a=(1,λ,2),b=(2,-1,2),且a与b夹角的余弦值为,则λ=()A.2B.-2C.-2或D.2或-4.已知a=(2,4,5),b=(3,x,y),若a∥b,则()A.x=6,y=15B.x=3,y=C.x=3,y=15D.x=6,y=5.若△ABC中,∠C=90°,A(1,2,-3k),B(-2,1,0),C(4,0,-2k),则k的值为()A.B.-C.2D.±6.正四棱柱ABCDA1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为()A.B.C.D.7.已知点A,B,C的坐标分别为(0,1,0),(-1,0,-1),(2,1,1),点P的坐标为(x,0,z),若PA⊥AB,PA⊥AC,则P点的坐标为__________.8.已知A,B,C三点的坐标分别是(2,-1,2),(4,5,-1),(-2,2,3),AP=(AB-AC),则点P的坐标是__________.9.已知向量a=(2,-1,2),则与a共线且a·x=-18的向量x=__________.10.如图所示,在正四棱柱ABCDA1B1C1D1中,O,O1分别为底面ABCD、底面A1B1C1D1的中心,AB=6,AA1=4,M为B1B的中点,N在C1C上,且C1N∶NC=1∶3.1(1)若以O为原点,分别以OA,OB,OO1所在直线为x轴、y轴、z轴建立空间直角坐标系,求图中各点的坐标;(2)若以D为原点,分别以DA,DC,DD1所在直线为x轴、y轴、z轴建立空间直角坐标系,求图中各点的坐标.11.如图所示,BC=2,原点O是BC的中点,点A的坐标为,点D在平面yOz内,且∠BDC=90°,∠DCB=30°.(1)求向量CD的坐标;(2)求向量AD与BC的夹角的余弦值.12.正四棱柱ABCDA1B1C1D1中,底面ABCD是边长为4的正方形,A1C1与B1D1交于点N,BC1与B1C交于点M,且AM⊥BN,建立空间直角坐标系.(1)求AA1的长;(2)求〈BN,AD1〉;(3)对于n个向量a1,a2,…,an,如果存在不全为零的n个实数λ1,λ2,…,λn,使得λ1a1+λ2a2+…+λnan=0成立,则这n个向量a1,a2,…,an叫做线性相关,不是线性相关的向量叫线性无关,判断AM,BN,CD是否线性相关,并说明理由.参考答案1.解析:设C(a,b,c),∵AB=(-3,-2,-4),∴(-3,-2,-4)=(a,b,c),∴(a,b,c)=.故选A.2答案:A2.解析:由题意,得M,则CM=,所以|CM|==.答案:C3.解析:a·b=2-λ+4=6-λ,|a|=,|b|=.cos〈a,b〉===.55λ2+108λ-4=0,解得λ=-2或λ=.答案:C4.解析:a∥b==答案:D5.解析:CB=(-6,1,2k),CA=(-3,2,-k),则CB·CA=(-6)×(-3)+2+2k(-k)=-2k2+20=0,∴k=±.答案:D6.解析:建立如图所示坐标系,由题意设A(1,0,0),B(1,1,0),D1(0,0,2),A1(1,0,2).由AD1=(-1,0,2),A1B=(0,1,-2),∴cos〈A1B,AD1〉==-.∴异面直线A1B与AD1所成角的余弦值为,故选D.答案:D7.解析:PA=(-x,1,-z),AB=(-1,-1,-1),AC=(2,0,1),∴∴∴P(-1,0,2).答案:(-1,0,2)8.解析:∵CB=(6,3,-4),设P(a,b,c),则(a-2,b+1,c-2)=,3∴a=5,b=,c=0,∴P.答案:9.解析:设x=(x,y,z),又a·x=-18,∴2x-y+2z=-18,①又∵a∥x,∴x=2λ,y=-λ,z=2λ,②由①②知,x=-4,y=2,z=-4,∴x=(-4,2,-4).答案:(-4,2,-4)10.解:(1)正方形ABCD中,AB=6,∴AC=BD=6,从而OA=OC=OB=OD=3.∴各点坐标分别为A(3,0,0),B(0,3,0),C(-3,0,0),D(0,-3,0),O(0,0,0),O1(0,0,4),A1(3,0,4),B1(0,3,4),C1(-3,0,4),D1(0,-3,4),M(0,3,2),N(-3,0,3).(2)同理A(6,0,0),B(6,6,0),C(0,6,0),D(0,0,0),A1(6,0,4),B1(6,6,4),C1(0,6,4),D1(0,0,4),O(3,3,0),O1(3,3,4),M(6,6,2),N(0,6,3).11.解:B(0,-1,0),C(0,1,0),CB=(0,-2,0).(1)由题意设D(0,m,n)(m<0,n>0),则BD=(0,m+1,n),CD=(0,m-1,n).因为∠BDC=90°,所以BD⊥CD,即(m-1)(m+1)+n2=0.①因为cos∠DCB===,②所以求解①②组成的方程组得或(舍去)或(舍去),所以D,所以CD=.(2)AD=,BC=(0,2,0),所以cos〈AD,BC〉===-,所以AD与BC的夹角的余弦值为-.12.解:(1)以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系.4设AA1的长为a,则B(4,4,0),N(2,2,a),BN=(-2,-2,a),A(4,0,0),M,AM=,由BN⊥AM得BN·AM=0,即a=2.(2)BN=(-2,-2,2),AD1=(-4,0,2),cos〈BN,AD1〉==,〈BN,AD1〉=arccos.(3)由AM=(-2,4,),BN=(-2,-2,2),CD=(0,-4,0),λ1(-2,4,)+λ2(-2,-2,2)+λ3(0,-4,0)=(0,0,0),得λ1=λ2=λ3=0,则AM,BN,CD线性无关.5