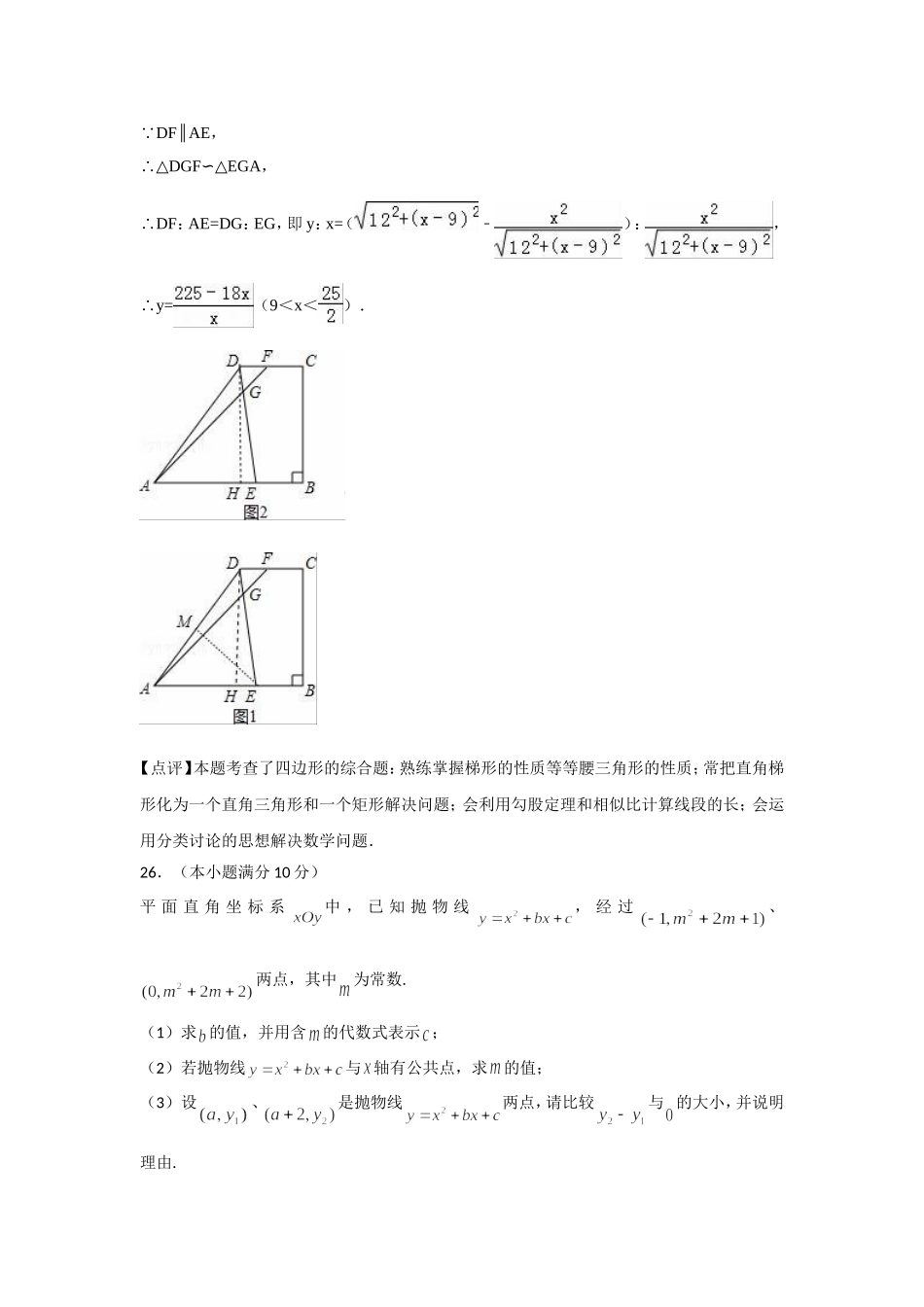
24.如图,抛物线y=ax2+bx5﹣(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.(1)求这条抛物线的表达式;(2)联结AB、BC、CD、DA,求四边形ABCD的面积;(3)如果点E在y轴的正半轴上,且∠BEO=ABC∠,求点E的坐标.25.如图所示,梯形ABCD中,ABDC∥,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=DAB∠.(1)求线段CD的长;(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.【解答】解:(1)作DHAB⊥于H,如图1,易得四边形BCDH为矩形,DH=BC=12∴,CD=BH,在RtADH△中,AH===9,BH=ABAH=169=7∴﹣﹣,CD=7∴;(2)当EA=EG时,则∠AGE=GAE∠,AGE=DAB∵∠∠,GAE=DAB∴∠∠,G∴点与D点重合,即ED=EA,作EMAD⊥于M,如图1,则AM=AD=,MAE=HAD∵∠∠,RtAMERtAHD∴△∽△,AE∴:AD=AM:AH,即AE:15=:9,解得AE=;当GA=GE时,则∠AGE=AEG∠,AGE=DAB∵∠∠,而∠AGE=ADG+DAG∠∠,∠DAB=GAE+DAG∠∠,GAE=ADG∴∠∠,AEG=ADG∴∠∠,AE=AD=15∴,综上所述,△AEC是以EG为腰的等腰三角形时,线段AE的长为或15;(3)作DHAB⊥于H,如图2,则AH=9,HE=AEAH=x9﹣﹣,在RtADE△中,DE==,AGE=DAB∵∠∠,∠AEG=DEA∠,EAGEDA∴△∽△,EG∴:AE=AE:ED,即EG:x=x:,EG=∴,DG=DEEG=∴﹣﹣,DFAE∵∥,DGFEGA∴△∽△,DF∴:AE=DG:EG,即y:x=(﹣):,y=∴(9<x<).【点评】本题考查了四边形的综合题:熟练掌握梯形的性质等等腰三角形的性质;常把直角梯形化为一个直角三角形和一个矩形解决问题;会利用勾股定理和相似比计算线段的长;会运用分类讨论的思想解决数学问题.26.(本小题满分10分)平面直角坐标系中,已知抛物线,经过、两点,其中为常数.(1)求的值,并用含的代数式表示;(2)若抛物线与轴有公共点,求的值;(3)设、是抛物线两点,请比较与的大小,并说明理由.考点:二次函数的图像和性质解析:(1)抛物线,经过、两点两式相减,得,(2)抛物线与轴有公共点,(3)抛物线对称轴为需分如下情况讨论:当时,由图像对称性得:,当时,,当时,,解法2:,当时,;当时,;当时,28.(本小题满分14分)如图,平面直角坐标系中,点,函数的图像经过□的顶点和边的中点.(1)求的值;(2)若的面积等于6,求的值.(3)若P为函数的图像上一个动点,过点P作直线轴于点M,直线与轴上方的□的一边交于点N,设点的横坐标为,当时,求的值.考点:值的几何意义,分类讨论思想解析:(1),,,由题意得:,,(第28题图)(2)过点作轴于点E,过点作轴于点F.由值的几何意义,得,即:,,则,将,代入,解得,则(3)设,直线与交于点N,,,,当时,即();化简得直线与AB交于点N,,,,当时,即,解得直线与BC交于点N,位于段,,,,,当时,即,化简得,(舍去)④直线与BC交于点N,位于段,,,,,当时,即,化简得,,(舍去)综上,,