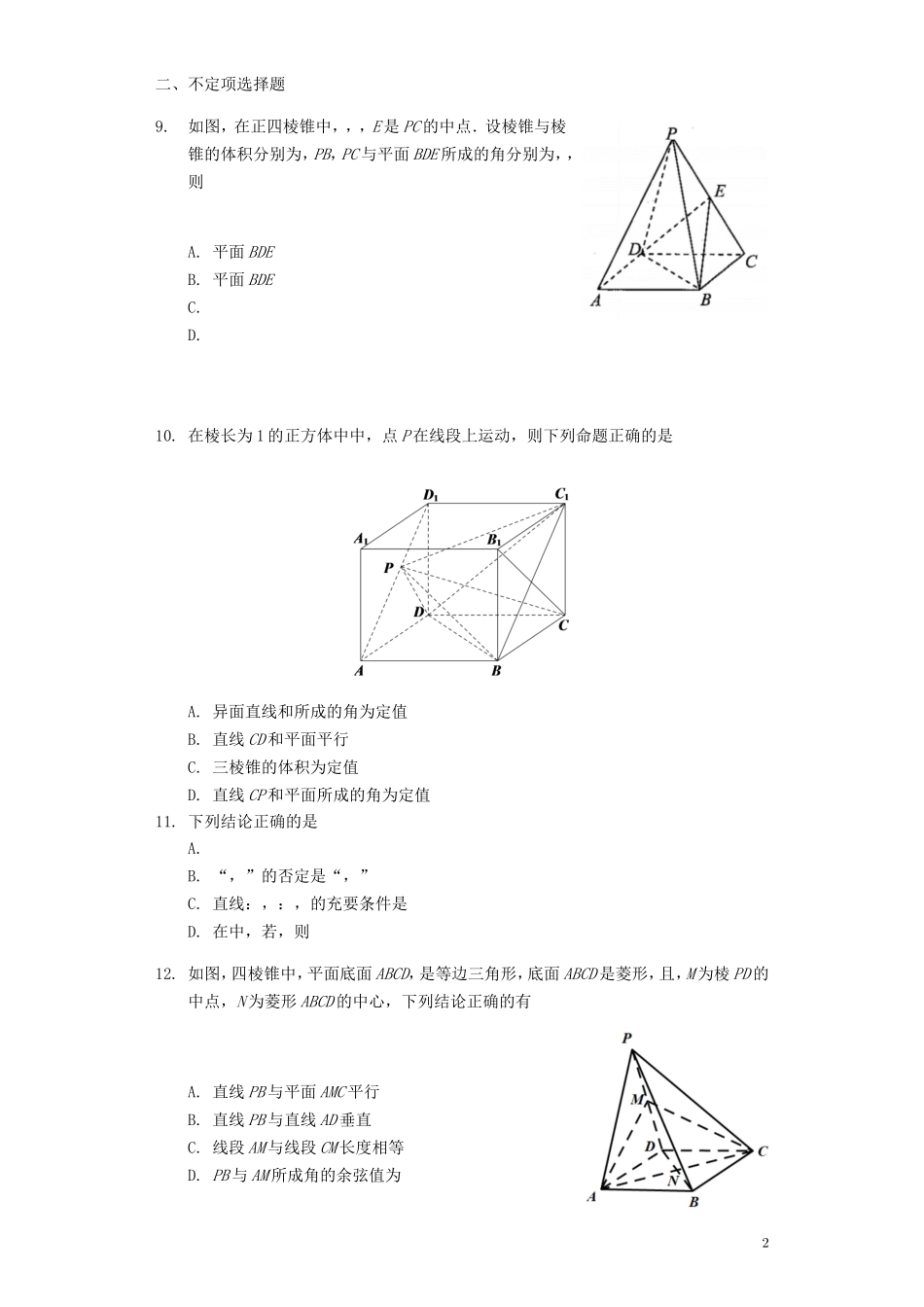
重庆市缙云教育联盟2020-2021学年高二数学9月月考试题注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。第I卷(选择题)一、选择题1.在三棱锥中,,,,则该三棱锥外接球的表面积为A.B.C.D.2.如图,在平行四边形ABCD中,沿AC将折成,记异面直线PA与BC所成的角为,直线PA与平面ABC所成的角为,二面角为,当时,则A.B.C.D.3.在四棱锥中,,,,,,,则三棱锥外接球的表面积为A.B.C.D.4.椭圆上的点P到直线l:的距离的最小值为A.B.C.D.5.在中,角A,B,C的对边分别为a,b,c,若角A,B,C成等差数列,且直线平分圆的周长,则的面积的最大值为A.B.C.D.6.已知三棱锥的外接球的球心为O,平面ABC,,,,则球心O到平面PBC的距离为A.B.C.D.7.已知球的直径,A、B是该球球面上的两点,,,则三棱锥的体积为A.B.3C.D.8.已知实数成等差数列,记直线与曲线的相交弦中点为P,若点分别是曲线与x轴上的动点,则的最小值是A.2B.3C.4D.51二、不定项选择题9.如图,在正四棱锥中,,,E是PC的中点.设棱锥与棱锥的体积分别为,PB,PC与平面BDE所成的角分别为,,则A.平面BDEB.平面BDEC.D.10.在棱长为1的正方体中中,点P在线段上运动,则下列命题正确的是A.异面直线和所成的角为定值B.直线CD和平面平行C.三棱锥的体积为定值D.直线CP和平面所成的角为定值11.下列结论正确的是A.B.“,”的否定是“,”C.直线:,:,的充要条件是D.在中,若,则12.如图,四棱锥中,平面底面ABCD,是等边三角形,底面ABCD是菱形,且,M为棱PD的中点,N为菱形ABCD的中心,下列结论正确的有A.直线PB与平面AMC平行B.直线PB与直线AD垂直C.线段AM与线段CM长度相等D.PB与AM所成角的余弦值为2第II卷(非选择题)三、填空题13.设点O为的外心,且,若,则的最大值为______.14.在三棱锥中,,,,二面角、、的大小均为,设三棱锥的外接球球心为O,直线SO交平面ABC于点M,则三棱锥的内切球半径为______,______.15.已知凸四边形指把四边形的任意一条边向两端无限延长成一直线时,其他各边都在此直线的同旁中,边,对角线,且,又顶点D满足,则凸四边形ABCD的对角线BD长的范围是.16.在棱长为6的正方体空盒内,有四个半径为r的小球在盒底四角,分别与正方体底面处交于某一顶点的三个面相切,另有一个半径为R的大球放在四个小球之上,与四个小球相切,并与正方体盒盖相切,无论怎样翻转盒子,五球相切不松动,则小球半径r的最大值为________;大球半径R的最小值为________.四、解答题17.如图,在四棱柱中,平面平面ABCD,底面ABCD是菱形,,E为的中点.证明:平面ACE;求直线与平面ACE所成角的正弦值.318.已知圆C:,直线l:.Ⅰ求证:对,直线l与圆C总有两个不同的交点;Ⅱ设l与圆C交于不同的两点A,B,求弦AB的中点M的轨迹方程;Ⅲ若定点分弦AB为,求此时直线l的方程.19.在中,角A,B,C的对边分别为a,b,c,在;;这三个条件中任选一个,补充在下面问题中,并作答.已知D是BC上的一点,,,,若____,求的面积.注:如果选择多个条件分别解答,按第一个解答计分.420.如图,椭圆C:的离心率,椭圆C的左、右顶点分别为A,B,又P,M,N为椭圆C上非顶点的三点.设直线PA,PB的斜率分别为,.求椭圆C的方程,并求的值;若,,判断的面积是否为定值?若为定值,求出该定值;若不为定值,请说明理由.21.如图,四棱锥中,侧面PAD是边长为2的等边三角形且垂直于底ABCD,是PD的中点.证明:直线平面PAB;点M在棱PC上,且直线BM与底面ABCD所成角为,求二面角的余弦值.22.已知圆,点,P是圆C上一动点,若线段PG的垂直平分线和CP相交于点M.求点M的轨迹方程E.5已知直线l:交曲线E于A,B两点.若射线BO交椭圆于点Q,求面积的最大值;若,OD垂直AB于点D,求点D的轨迹方程.6答案和解析1.【答案】C【解析】解:由题意可将该三棱锥放在长方体中,可得长方体的过同一个顶点的三个相邻的面的对角线分别为5,,,设长方体的长,宽,高分别为a,b,c,则,所以,设三棱锥外接球的半径为R,则,属于外接球的表面...