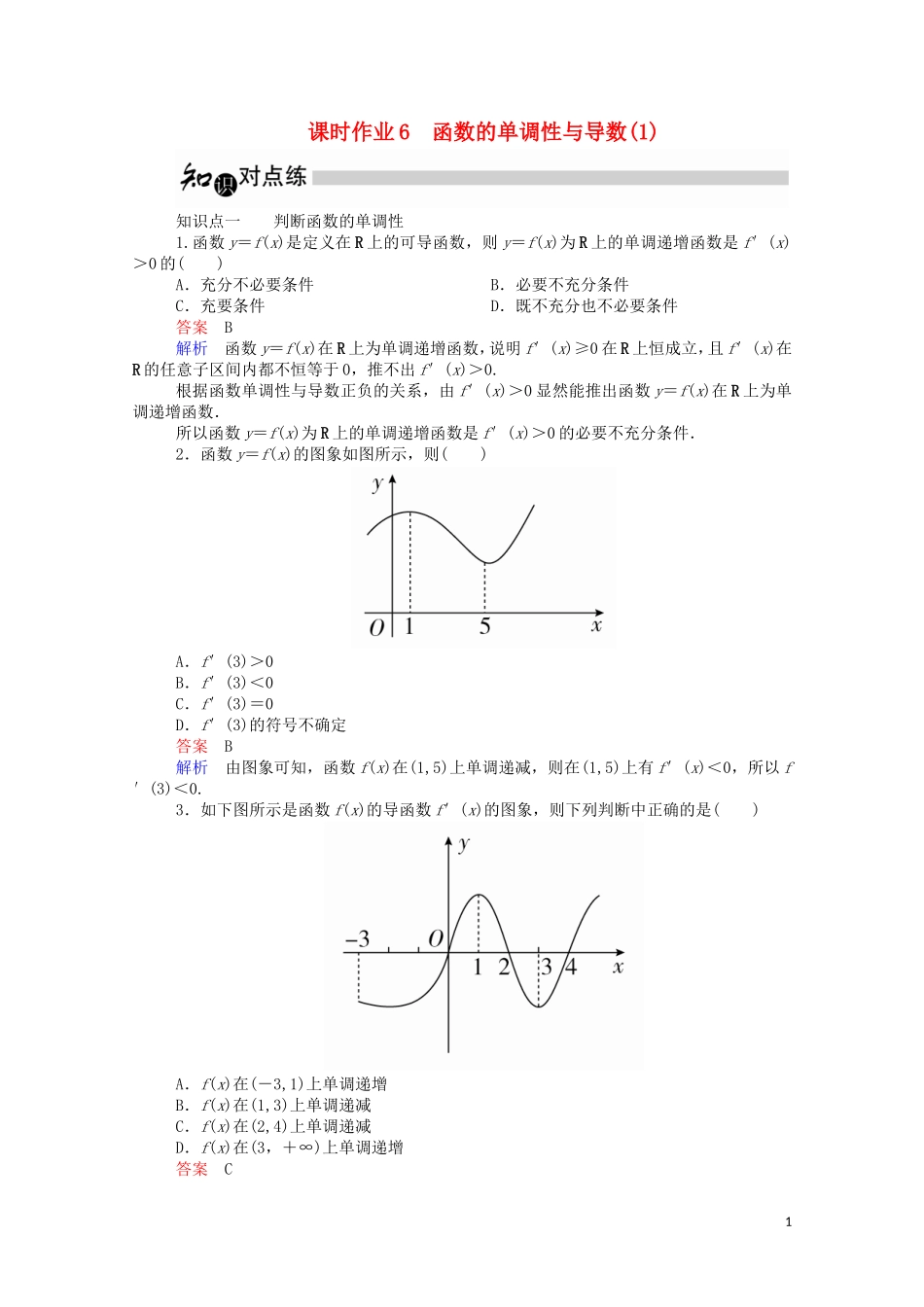
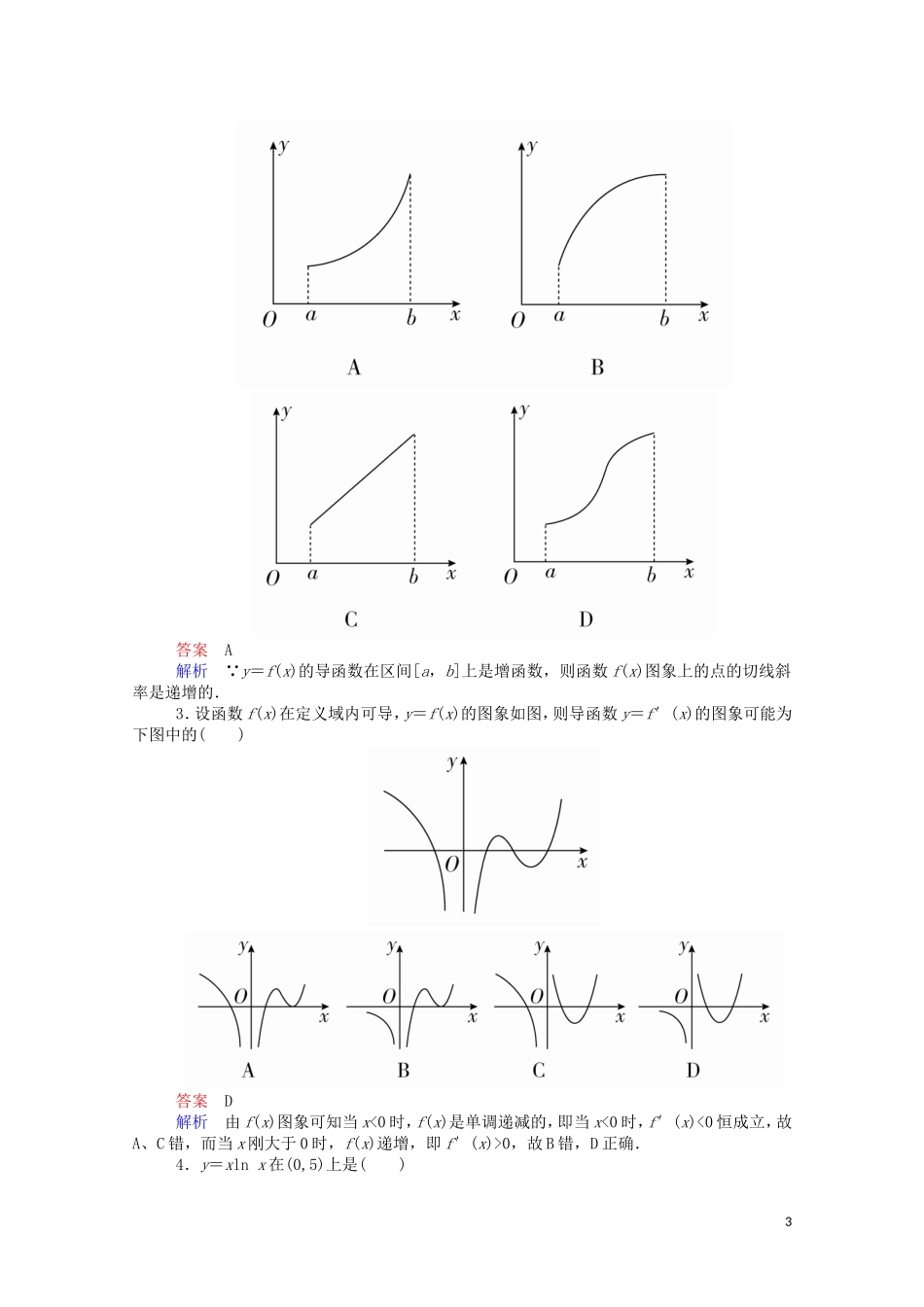
课时作业6函数的单调性与导数(1)知识点一判断函数的单调性1.函数y=f(x)是定义在R上的可导函数,则y=f(x)为R上的单调递增函数是f′(x)>0的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案B解析函数y=f(x)在R上为单调递增函数,说明f′(x)≥0在R上恒成立,且f′(x)在R的任意子区间内都不恒等于0,推不出f′(x)>0.根据函数单调性与导数正负的关系,由f′(x)>0显然能推出函数y=f(x)在R上为单调递增函数.所以函数y=f(x)为R上的单调递增函数是f′(x)>0的必要不充分条件.2.函数y=f(x)的图象如图所示,则()A.f′(3)>0B.f′(3)<0C.f′(3)=0D.f′(3)的符号不确定答案B解析由图象可知,函数f(x)在(1,5)上单调递减,则在(1,5)上有f′(x)<0,所以f′(3)<0.3.如下图所示是函数f(x)的导函数f′(x)的图象,则下列判断中正确的是()A.f(x)在(-3,1)上单调递增B.f(x)在(1,3)上单调递减C.f(x)在(2,4)上单调递减D.f(x)在(3,+∞)上单调递增答案C1解析由f(x)的增减性与f′(x)的正负之间的关系进行判断,当x∈(2,4)时,f′(x)<0,故f(x)在(2,4)上单调递减,其余判断均错.4.求证:函数f(x)=ex-x-1在(0,+∞)内是增函数,在(-∞,0)内是减函数.证明由于f(x)=ex-x-1,所以f′(x)=ex-1,当x∈(0,+∞)时,ex>1,即f′(x)=ex-1>0,故函数f(x)在(0,+∞)内为增函数;当x∈(-∞,0)时,ex<1,即f′(x)=ex-1<0,故函数f(x)在(-∞,0)内为减函数.知识点二求函数的单调区间5.函数f(x)=(x-3)ex的单调递增区间是()A.(-∞,2)B.(0,3)C.(1,4)D.(2,+∞)答案D解析f′(x)=(x-3)′ex+(x-3)(ex)′=ex(x-2).由f′(x)>0得x>2,∴f(x)的单调递增区间是(2,+∞).6.函数y=x2-lnx的单调递减区间为()A.(-1,1]B.(0,1]C.[1,+∞)D.(0,+∞)答案B解析函数y=x2-lnx的定义域为(0,+∞),y′=x-=,令y′≤0,则可得00,则2x(x-2)>0,解得x<0或x>2.所以函数的单调递增区间为(-∞,0),(2,+∞).令y′<0,则2x(x-2)<0,解得00,解得--.所以函数的单调递增区间为,.令y′<0,解得-10,故B错,D正确.4.y=xlnx在(0,5)上是()3A.单调增函数B.单调减函数C.在上单调递减,在上单调递增D.在上单调递增,在上单调递减答案C解析 y′=x′·lnx+x·(lnx)′=lnx+1,∴当0-1,即y′>0,∴y在上单调递增.5.函数f(x)=ax3-x在R上为减函数,则()A.a≤0B.a<1C.a<2D.a≤答案A解析f′(x)=3ax2-1. f(x)在R上为减函数,∴f′(x)≤0在R上恒成立.∴a≤0,经检验a=0符合题意.二、填空题6.函数y=f(x)在定义域内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)<0的解集为________.答案∪(2,3)解析f′(x)<0的解集即为f(x)的单调递减区间,结合题图可知f′(x)<0的解集为∪(2,3).7.函数y=ln(x2-x-2)的递减区间为__________.答案(-∞,-1)解析 f′(x)=,由f′(x)=<0,得x<-1或