高二数学平面的画法及表示人教版知识精点VIP免费

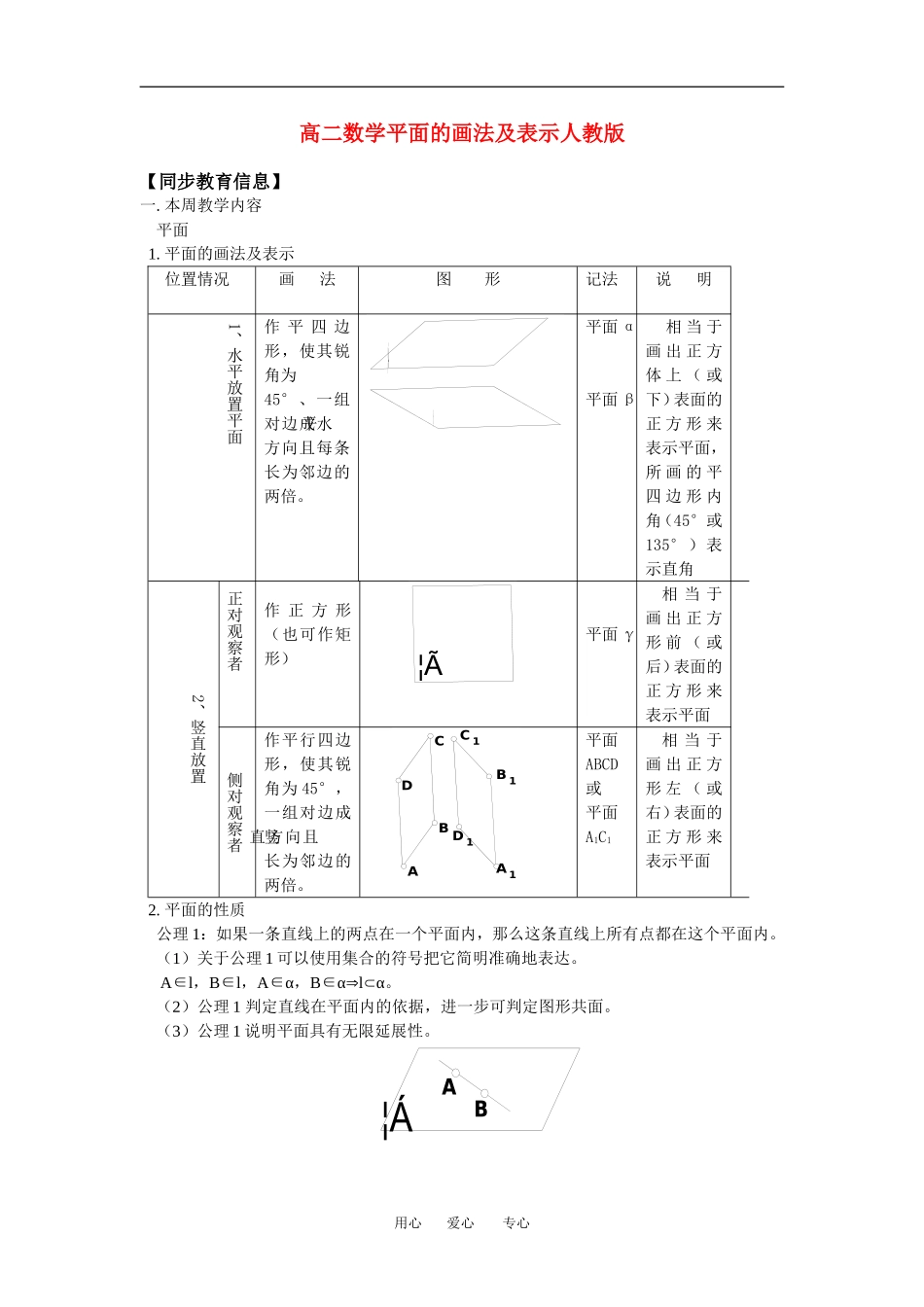
高二数学平面的画法及表示人教版【同步教育信息】一.本周教学内容平面1.平面的画法及表示位置情况画法图形记法说明1、水平放置平面作平四边形，使其锐角为45°、一组对边成水平方向且每条长为邻边的两倍。β¦Á平面α平面β相当于画出正方体上（或下）表面的正方形来表示平面，所画的平四边形内角（45°或135°）表示直角2、竖直放置正对观察者作正方形（也可作矩形）¦Ã平面γ相当于画出正方形前（或后）表面的正方形来表示平面侧对观察者作平行四边形，使其锐角为45°，一组对边成竖直方向且长为邻边的两倍。CDABC1D1A1B1平面ABCD或平面A1C1相当于画出正方形左（或右）表面的正方形来表示平面2.平面的性质公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有点都在这个平面内。（1）关于公理1可以使用集合的符号把它简明准确地表达。A∈l，B∈l，A∈α，B∈αlα。（2）公理1判定直线在平面内的依据，进一步可判定图形共面。（3）公理1说明平面具有无限延展性。BA¦Á用心爱心专心公理2：如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线。如图：l¦Â¦Á强调：1.“有且只有一条”的含义是：“有”说明直线是存在的，“只有”说明直线是唯一的。2.如果两个平面α和β有一条公共直线，就说平面α和β相交，交线是a，则可记作α∩β＝a3.公理2可表示成如下形式：若A∈α，A∈β，则α∩β＝a，且A∈a。4.两个平面如果有一个公共点，那么就有无穷多个公共点，所有公共点在公共直线上，即它们的交线上；交线的每一个点都是两个平面的公共点。5.公理2是作出两个平面交线的依据。6.在公理指导下画出两个相交平面的一般步骤如下：①先画表示两个平面的平行四边形的相交两边，如图（1）②再画出表示两个平面交线的线段，如图（2）③过图（1）中线段的端点分别引线段，使它平行且等于（2）中表示交线的线段，如图（3）。④画图中表示两个平面的平行四边形的第四边（被遮住的线，可以用虚线，也可以不画，如图（4））（1）（2）（3）（4）公理3：经过不在同一条直线上的三点，有且只有一个平面。强调：①公理3实际上是给出了确定平面的条件。讲解是应突出“不在同一直线上”和“三点”几个字②“有且只有”的理解：“有”说明直线是存在的；“只有”说明直线是唯一的。公理3推论推论1经过一条直线和这条直线外一点，有且只有一个平面。推论2经过两条相交直线，有且只有一个平面推论3经过两条平行直线，有且只有一个平面强调：①会用符号表达推论内容（见下表）名称符号表示图形用心爱心专心推论1Aa有且只有一个平面α，使A∈α，aαABC¦Á推论2a∩b＝P有且只有一个平面α，使aα，bαba¦Á推论3a∥b有且只有一个平面α，使aα，bα¦Á②会证明三条推论：先证“有”，再证“只有”，即证明存在性和唯一性③明确三条推论的作用：同公理3一样是确定平面的依据。【典型例题】例1、⑴画出经过已知直线AB的三个平面。⑵已知三条直线a、b、c两两平行但不共面（即不在同一平面内），画出这些平面。思路与解：如下图bcaAB¦Á¦Â¦Ã¦Â¦Á¦Ã（甲）（乙）甲图设计各平面绕直线AB转动情况；乙图设计整个图形转动。请同学们观察作出相交平面应该注意的问题。例2.三个不同平面可能把空间分成几部分？画图说明可能分成4，6，7，8个部分。引例：三条直线把平面分成4、6、7部分。（1）四部分（互相平行）（2）六部分（两种情况）用心爱心专心（3）七部分（4）八部分例3.已知：延长⊿ABC三边，AB＝D，BC＝E，AC＝F，求证：D、E、F共线。思路与解：如图分析：只需证明这三点都是某两个平面的公共点。ADFCEB¦Á证明： ⊿ABC是一平面图形，所在的平面为β D∈α且D∈ABβ∴D是α、β的公共点，同理，E、F也是α、β的公共点∴D、E、F都在α、β的交线上，即这三点共线例4.已知：直线a//b，直线c和a、b都相交，直线d也和a、b都相交。求证：c、d可以确定一个平面。思路与解：如图设直线c和直线a、b的交点分别为A、B；直线d和直线a、b的交点分别为C、D a//b，∴a、b可以确定一个平面 A∈α，B∈α，A∈c，B∈c，∴cα同理dα∴d、c在...