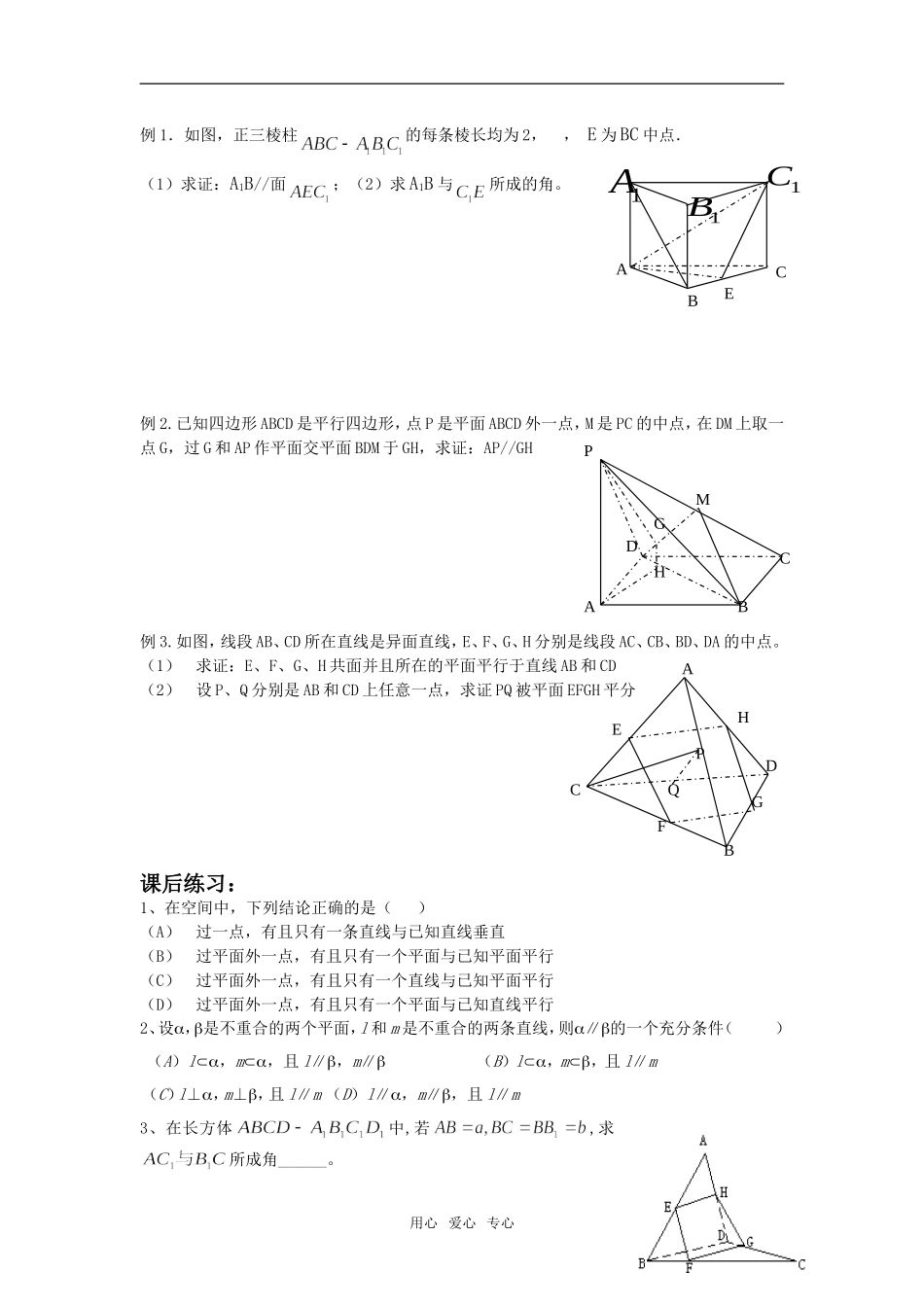
直线与平面、平面与平面平行考查知识点:1.求异面直线所成角2.平行的线面关系的证明及应用一:知识点回顾:1.点A在直线上可表示为;点A在直线外可表示为;点A在平面内可表示为;点A在平面外可表示为;直线在平面内可表示为;直线在平面外可表示为。2.若,,则。3.公理1:。用符号语言可表示为:。4.公理2:。5.公理3:。推论1:;推论2:;推论3:。6.空间两直线的三种位置关系:(1)相交直线---;(2)平行直线---;(3)异面直线---。7.等角定理:。8.直线是异面直线,经过空间任意一点,作直线,使,,我们把直线和所成的叫作异面直线所成的角.9.如果两条异面直线所成的角是,我们就说这两条异面直线垂直,两条异面直线所成角的范围是.10.一条直线与一个平面的位置关系有。11如果一条直线,那么这条直线和这个平面平行。.12.证明直线与平面平行的步骤:(1)先说明直线平面;(2)再在平面内找到,并证明直线与它,由直线和平面的得。13、两平面的位置关系有:(1)平行——;(2)相交——。二:方法总结1.异面直线的判定方法:(1)反证法;(2)判定定理:(文字语言)2.线线平行的判定方法:(1)平行公理:。(用符号表示)(2)直线与平面平行的性质定理:用心爱心专心高二期末复习专题之五文字语言___________。符号语言___简称“线面平行,则线(外)线(交线)平行”。(3)平面与平面平行性质定理:文字语言;符号语言_____简称“面面平行,则线线(交线)平行”。3.直线与平面平行的判定方法:(1)定义:;(2)直线与平面平行的判定定理:文字语言_________。符号语言_____简称“线(外)线(内)平行,则线面平行”。(3)面面平行的性质:如果两个平面平行,那么其中一个平面内的直线平行与另一个平面;符号语言____简称“面面平行,则线面平行”4.平面与平面平行的判定方法:(1)定义:;(2)面面平行的判定定理:文字语言;符号语言。(3)面面平行判定的推论:文字语言;符号语言。三:基础训练1、空间四点中“三点共线”是“四点共面”的()条件A、充分不必要B、必要不充分C、充分且必要D、既不充分也不必要2、在棱长为的正方体中,M,N,P,Q是相应棱的中点,则:(1)MN与PQ的位置关系是;它们所成角是.(2)MN与的位置关系是;它们所成角是.3、有如下命题;①若直线②若直线③若直线④若直线其中正确的命题是()(A)①、④(B)①、③(C)②(D)均不正确四、例题分析:用心爱心专心D1C1B1A1QPNMDCBA例1.如图,正三棱柱的每条棱长均为2,,E为BC中点.(1)求证:A1B//面;(2)求A1B与所成的角。例2.已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP//GH例3.如图,线段AB、CD所在直线是异面直线,E、F、G、H分别是线段AC、CB、BD、DA的中点。(1)求证:E、F、G、H共面并且所在的平面平行于直线AB和CD(2)设P、Q分别是AB和CD上任意一点,求证PQ被平面EFGH平分课后练习:1、在空间中,下列结论正确的是()(A)过一点,有且只有一条直线与已知直线垂直(B)过平面外一点,有且只有一个平面与已知平面平行(C)过平面外一点,有且只有一个直线与已知平面平行(D)过平面外一点,有且只有一个平面与已知直线平行2、设,是不重合的两个平面,l和m是不重合的两条直线,则∥的一个充分条件()(A)l,m,且l∥,m∥(B)l,m,且l∥m(C)l⊥,m⊥,且l∥m(D)l∥,m∥,且l∥m3、在长方体中,若,求所成角______。用心爱心专心AEBC1A1B1CABDCPMGHACBDEHFGPQ4、(如右图)空间四边形ABCD中,E、H分别是AB、AD的中点,F、G分别是CB、CD上的点,且,若BD=6,梯形EFGH的面积是28,则平行线EH、FG间的距离是______。5、P是平行四边形ABCD所在平面外一点,Q是PA中点,求证:PC∥平面BDQ。6、已知两条异面直线a,b分别与三个平行平面α,β,γ相交于点A,B,C和P,Q,R,又AR,CP与平面β相交于点M,N,求证:MBNQ为平行四边形。用心爱心专心R