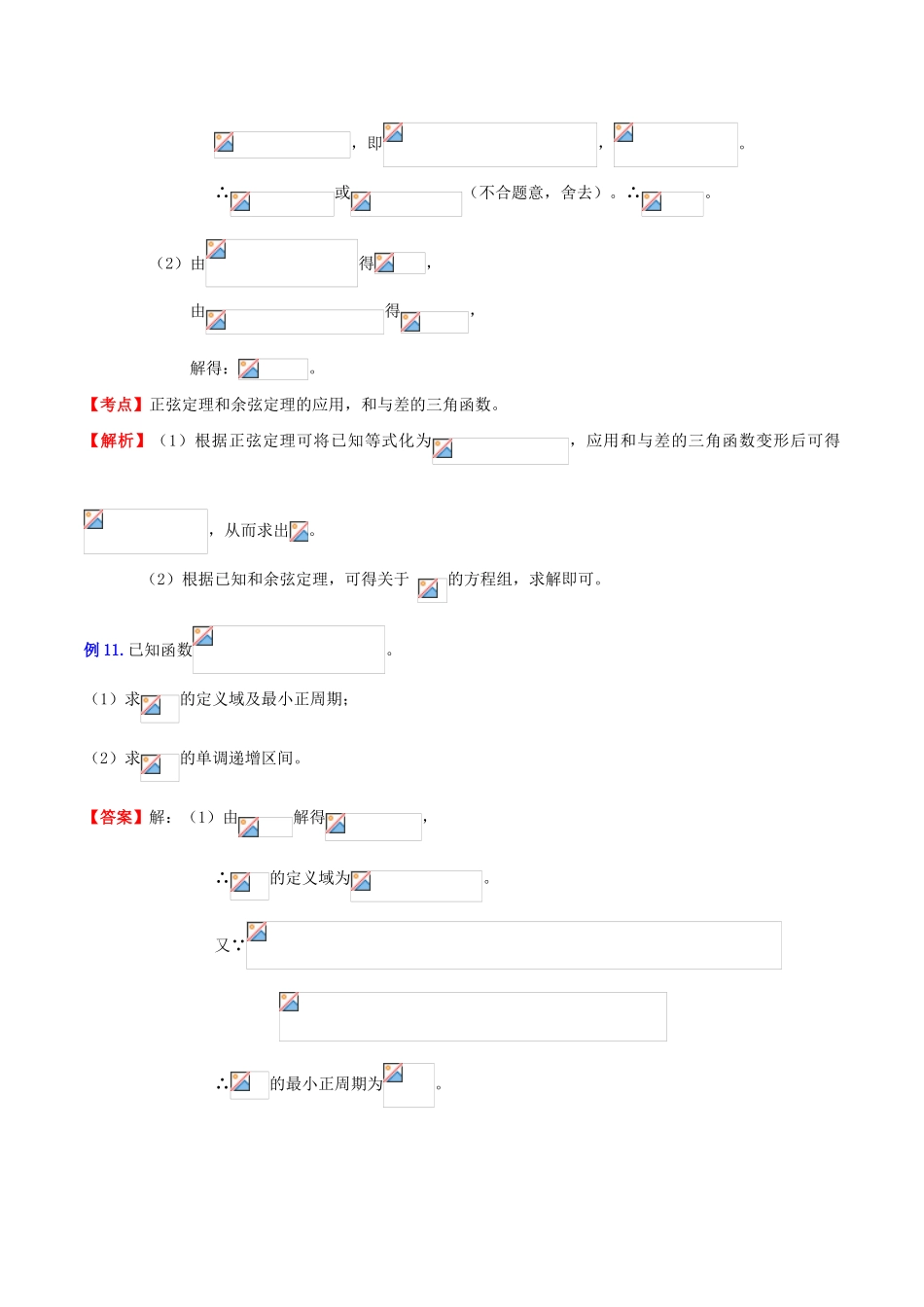
(新课标)高考数学一轮复习名校尖子生培优大专题三角函数之三角函数的综合问题2新人教A版例9.已知分别为三个内角的对边,(1)求(2)若,的面积为;求。【答案】解:(1)由,根据正弦定理得:,∵,∴。∴。∴。∴或(不合题意,舍去)。∴。(2)由得,由得,解得:。【考点】正弦定理和余弦定理的应用,和与差的三角函数。【解析】(1)根据正弦定理可将已知等式化为,应用和与差的三角函数变形后可得,从而求出。(2)根据已知和余弦定理,可得关于的方程组,求解即可。例10.已知a,b,c分别为△ABC三个内角A,B,C的对边,c=asinC-ccosA(1)求A(2)若a=2,△ABC的面积为,求b,c【答案】解:(1)由c=asinC-ccosA得,根据正弦定理,得,即,。∴或(不合题意,舍去)。∴。(2)由得,由得,解得:。【考点】正弦定理和余弦定理的应用,和与差的三角函数。【解析】(1)根据正弦定理可将已知等式化为,应用和与差的三角函数变形后可得,从而求出。(2)根据已知和余弦定理,可得关于的方程组,求解即可。例11.已知函数。(1)求的定义域及最小正周期;(2)求的单调递增区间。【答案】解:(1)由解得,∴的定义域为。又∵∴的最小正周期为。(2)∵,∴根据正弦函数的增减性,得或,。解得或,。∴的单调递增区间为。【考点】三角函数的定义域、最小正周期和单调增减性。【解析】(1)根据分式分母不为0的条件,结合正弦函数的零点得出的定义域。将变形,即可由求最小正周期的公式求得。(2)根据正弦函数的增减性,结合的定义域,求出的单调递增区间。例12.函数在一个周期内的图象如图所示,为图象的最高点,、为图象与轴的交点,且为正三角形。(Ⅰ)求的值及函数的值域;(Ⅱ)若,且,求的值。【答案】解:(Ⅰ)由已知可得:又∵正的高为2,∴BC=4。∴函数的同期,即,解得。∴函数的值域为。(Ⅱ)∵,由(Ⅰ)有,即。由得x0。∴∴。【考点】三角函数的图像与性质,同角三角函数的关系、两角和的正(余)弦公式、二倍角公式。【解析】(Ⅰ)将)化简为,利用正弦函数的周期公式与性质可求的值及函数的值域。(Ⅱ)由,知,由,可求得即,利用两角和的正弦公式即可求得。例13.已知函数。(Ⅰ)求函数的最小正周期和值域;(Ⅱ)若,求的值。【答案】解:(Ⅰ)∵,∴的最小正周期为2,值域为。(Ⅱ)由(Ⅰ)知,=,∴cos。∴。【考点】三角函数的性质、两角和的正(余)弦公式、二倍角公式。【解析】(Ⅰ)将化为即可求得的最小正周期和值域。(Ⅱ)由=可求得cos,由余弦函数的二倍角公式与诱导公式可求得的值。例14.已知函数,.(Ⅰ)求函数的最小正周期;(Ⅱ)求函数在区间上的最大值和最小值.【答案】解:(Ⅰ)∵,∴函数的最小正周期。(Ⅱ)∵函数在区间上是增函数,在区间上是减函数,又,∴函数在的最大值为2,最小值为-1。【考点】三角函数中的恒等变换应用,三角函数的周期性及其求法,三角函数的最值。【分析】(Ⅰ)利用正弦函数的两角和与差的公式与辅助角公式将化为,即可求得函数的最小正周期。(Ⅱ)分析得到函数在区间上的增减性,即可是求得在区间的最大值和最小值。例15.在中,内角所对的分别是。已知,.(I)求和b的值;(II)求的值。【答案】解:(I)在中,∵,∴。∵,,∴。∵,∴,解得。(II)∵、∴,。∴。【考点】解三角形,三角函数中的恒等变换应用。【分析】(I)中,利用同角三角函数的基本关系求出,再由正弦定理求出,再由余弦定理求得。(II)利用二倍角公式求得和的值,,再由两角和的余弦公式求出的值。例16.设函数(I)求函数的最小正周期;(II)设函数对任意,有,且当时,;求函数在上的解析式。【答案】解:(I)∵,∴函数的最小正周期。(II)∵当时,∴当时,,当时,,。∴函数在上的解析式为。【考点】三角函数公式和性质。,【解析】(I)将化为,即可求出函数的最小正周期。(II)由得出关于的函数关系式。由分区间讨论即可。