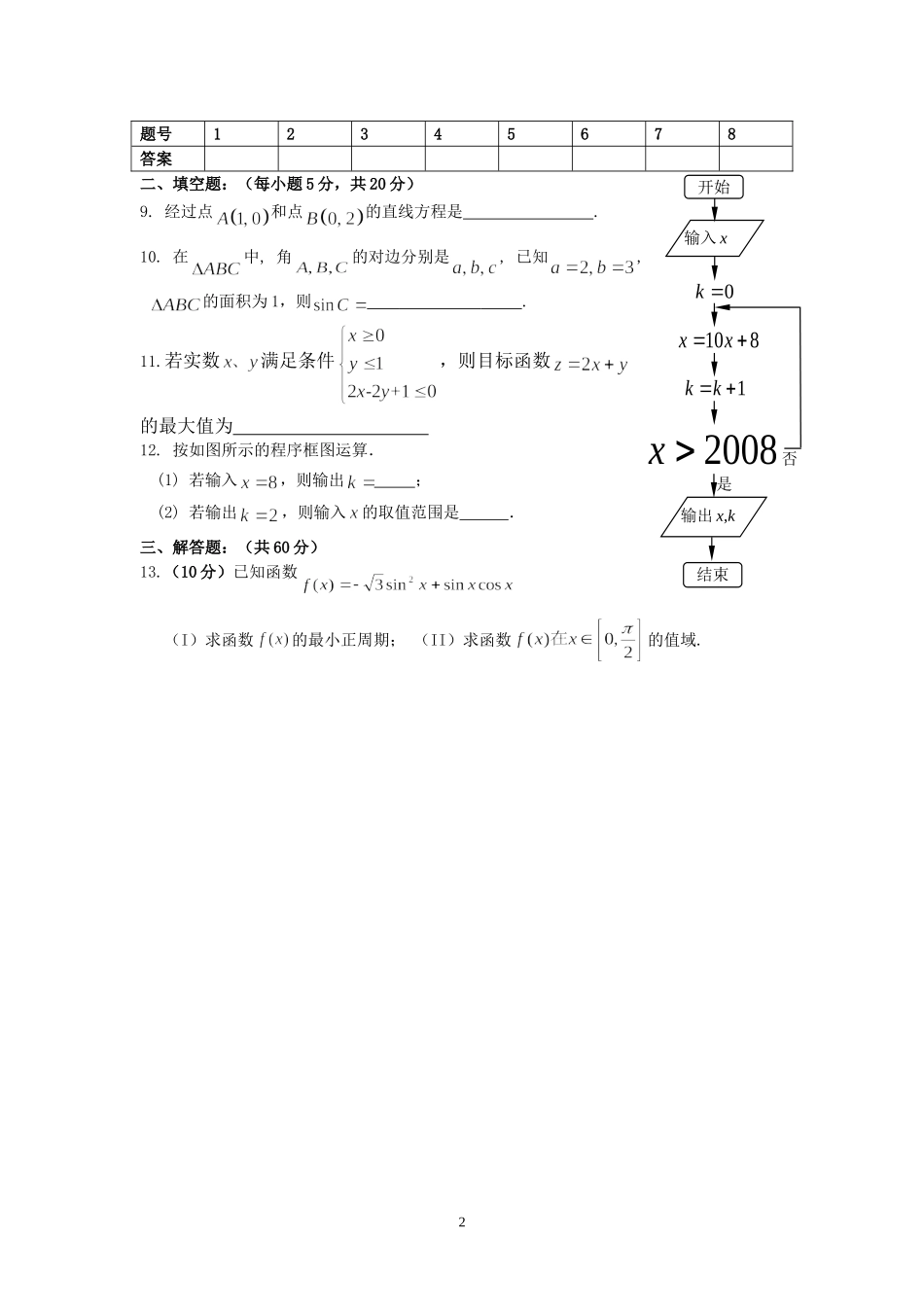
高二数学(理)每周一测(11)(08.11.23)一、选择题:(本大题共10小题,每小题5分,共40分)1.若焦点在轴上的椭圆的离心率为,则m=A.B.C.D.2.直线的斜率是A.B.C.D.3.袋子中装有红、白、黄颜色且大小相同的小球各一个.从袋子中任意取出一球,则取出的是红球的概率是A.B.C.D.4.已知集合,则A.B.C.D.5.已知等比数列的公比是2,,则的值是A.B.C.4D.166.在中,为边的中点,设,,则A.B.C.D.7.设,实数满足,则关于的函数的图象大致形状是8.是方程至少有一个负数根的A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件班别:姓名:学号:1ABCD题号12345678答案二、填空题:(每小题5分,共20分)9.经过点和点的直线方程是.10.在中,角的对边分别是,已知,的面积为1,则.11.若实数满足条件,则目标函数的最大值为12.按如图所示的程序框图运算.(1)若输入,则输出;(2)若输出,则输入的取值范围是.三、解答题:(共60分)13.(10分)已知函数(I)求函数的最小正周期;(II)求函数的值域.2开始0k108xx1kk结束输入x是否输出x,k2008x14.(12分)在递增等差数列中,已知,且、、成等比数列,.(I)求数列的公差;(Ⅱ)设数列的前项和为,求的最值.15.(12分)已知三棱柱ABC—A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,(1)在三棱柱ABC—A1B1C1中,求证:BC⊥AC1;(2)在三棱柱ABC—A1B1C1中,若D是底边AB的中点,求证:AC1∥平面CDB1.(3)若三棱柱的高为5,求三视图中左视图的面积.3B1A1C1俯视图主视图左视图BB1A1AAA1C1CCCBB1C1BB1C1D16.(12分)设、分别是椭圆的左、右焦点.(Ⅰ)若是该椭圆上的一个动点,求·的最大值和最小值;(Ⅱ)设过定点的直线与椭圆交于不同的两点、,求直线的斜率的取值范围.17.(14分)已知函数.(Ⅰ)当时,求函数的最小值;(Ⅱ)若对任意,恒成立,试求实数的取值范围.4高二数学(理)每周一测(11)(08.11.23)参考答案题号12345678答案BACBCAAB9.10.11.212.(1)3;(2)13.解:(I)函数的最小正周期是……………………………5分(II)∴∴∴所以的值域为:……10分14.解:(I)、、成等比数列………………………………2分………………………………4分整理得:,解得或………………………………5分又递增………………………………6分(Ⅱ)由,得………………………………8分令得:,且………………………………11分所以前6项或者前7项的和最小,无最大值………………………………12分15.(1)因为主视图和左视图均为矩形、所以该三棱柱为直三棱柱,在俯视图△A1B1C1中,A1C1=3,A1B1=5,,由余弦定理可得,∴,5∴又∵BC⊥CC1,CC1∩A1C1=C1,∴BC⊥平面ACC1A1.∵AC1平面ACC1A1,∴BC⊥AC1.(2)连BC1交B1C于M,则M为BC1的中点,连DM,则DM∥AC1.∵DM平面DCB1,AC1平面DCB1,∴AC1∥平面CDB1.(3)左视图中BC的长等于底面△ABC中顶点C到边AB的距离d,,∴左视图的面积.16.解:(Ⅰ)解法一:易知,所以…………1分,设,则…………3分因为,故当,即点为椭圆短轴端点时,有最小值……5分当,即点为椭圆长轴端点时,有最大值…………7分解法二:易知,所以…………1分,设,则…………3分(以下同解法一)(Ⅱ)显然直线不满足题设条件…………8分,可设直线,联立,消去,整理得:…………9分6由>0得:…………12分17.解:(1),当时,取得等号……………………6分(Ⅱ)……………………9分……………………12分.∴的取值范围是……………………14分7