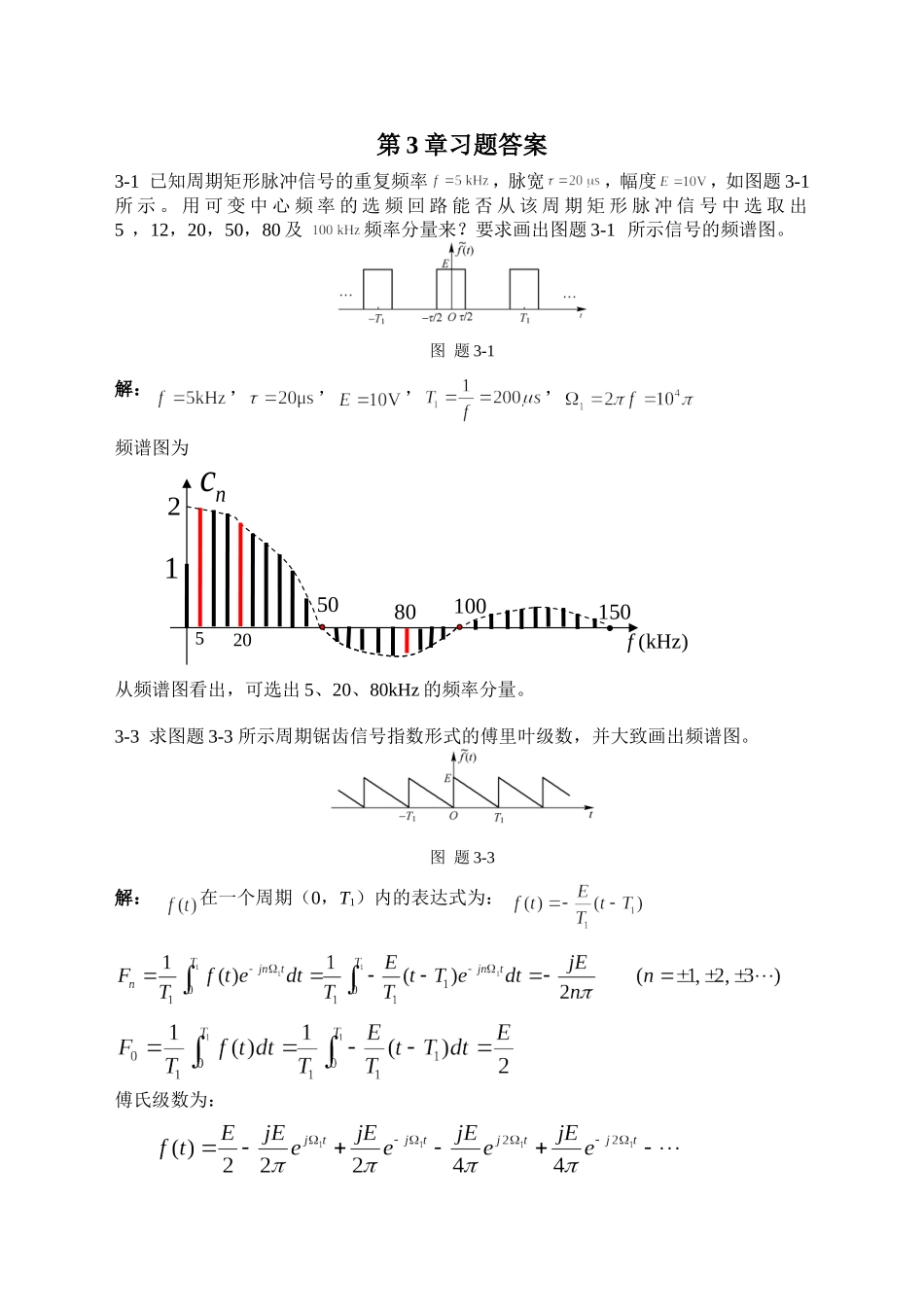
第3章习题答案3-1已知周期矩形脉冲信号的重复频率,脉宽,幅度,如图题3-1所示。用可变中心频率的选频回路能否从该周期矩形脉冲信号中选取出5,12,20,50,80及频率分量来?要求画出图题3-1所示信号的频谱图。图题3-1解:,,,,频谱图为从频谱图看出,可选出5、20、80kHz的频率分量。3-3求图题3-3所示周期锯齿信号指数形式的傅里叶级数,并大致画出频谱图。图题3-3解:在一个周期(0,T1)内的表达式为:傅氏级数为:nc12(kHz)f5205010015080频谱图为:3-4求图题3-4所示半波余弦信号的傅里叶级数,若,,大致画出幅度谱。图题3-4解:由于是偶函数,所以展开式中只有余弦分量,故傅氏级数中,另由图可知有直流分量,在一个周期(,)内的表达式为:其中:nF2E6E10E11315113154E12148E2E121422n151311131512121414所以,的三角形式的傅里叶级数为:3-6利用信号的对称性,定性判断图题3-6中各周期信号的傅里叶级数中所含有的频率分量。图题3-6解:(a)为偶函数及奇谐函数,傅氏级数中只包含奇次谐波的余弦分量。nc12E23E215E1213141516171819110E(b)为奇函数及奇谐函数,傅氏级数中只包含奇次谐波的正弦分量。(c)为偶谐函数,而且若将直流分量(1/2)去除后为奇函数,所以傅氏级数中只包含直流以及偶次谐波的正弦分量。(d)为奇函数,傅氏级数中只包含正弦分量。(e)为偶函数及偶谐函数,傅氏级数中只包含直流以及偶次谐波的余弦分量。(f)为奇谐函数,傅氏级数中只包含奇次谐波分量。3-7已知周期函数前四分之一周期的波形如图题3-7所示。根据下列各种情况的要求画出在一个周期()的波形。(1)是偶函数,只含有直流分量和偶次谐波分量;(2)是偶函数,只含有奇次谐波分量;(3)是偶函数,含有直流分量、偶次和奇次谐波分量。解:(1)由画出在内的波形,由在内的波形及是偶谐函数,它在内的波形与它在内的波形相同,它在内的波形与它在内的波形相同。根据上述分析可画出在内的波形。按上述类似的方法可画出(2)和(3)。(2)t()ft4T02TTt()ft4T0T图题3-7(3)3-8求图题3-8所示半波余弦脉冲的傅里叶变换,并画出频谱图。图题3-8解法一:按定义求由于是偶函数,所以化简得:解法二:利用卷积定理求设:则,于是而,t()ft4T02TT34T故的频谱是将矩形脉冲的频谱分别向左、右移动(幅度乘以)后叠加的结果。3-10求图题3-10所示的傅里叶逆变换。图题3-10解:(a)(b))(ΩjF33Ω55/2E2/E3-13求函数的傅里叶变换。解:利用对偶性求因为,所以令,则即:F3-15对图题3-15所示波形,若已知,利用傅里叶变换的性质求图中,和的傅里叶变换。图题3-15解:已知F,,3-21已知三角脉冲信号如图题3-21(a)所示。试利用有关性质求图题3-21(b)中的的傅里叶变换。图题3-21解:设F则F而FF=3-23利用傅里叶变换的微分与积分特性,求图题3-23所示信号的傅里叶变换。图题3-23解:(3)3-25若已知,利用傅里叶变换的性质求下列信号的傅里叶变换。(2)(4)(5)解:(2)FF(4)F(5)FF3-29根据附录B中给出的频谱公式,粗略地估计图题3-29所示各脉冲的频带宽度(图中时间单位为)。图题3-29解:(a)若时间单位为,则频带为MHz,即250KHz(b)若时间单位为,则频带为MHz,即250KHz(d)若时间单位为,则频带为1MHz(f)频若时间单位为,则带为MHz,即500KHz3-32周期矩形脉冲信号如图题3-32所示。(1)求的指数形式的傅里叶级数,并画出频谱图;(2)求的傅里叶变换,并画出频谱图。图题3-32解:(1)指数形式的傅里叶级数为:频谱图如下图所示,图中:(2)F频谱图为3-33求下列函数的拉氏变换,设。(1)(4)(6)(8)解:(1)(4)1131511315()()Fj1214nF1131411315121215(6)(8)3-35求下列函数的拉氏变换,注意阶跃函数的跳变时间。(1)(2)(3)解:(1)2(2)(2)(2)tteuteeut(2)2(2)(2)(2)tteuteeut(3)3-39求下列函数的单边拉普拉斯逆变换。(3)(4)(7)解:(3)(4)(7)3-40试利用拉氏变换的时域卷积定理求下列拉氏变换的原函数。(1)解:所以3-43分别求下列函数的逆变换之初值和终值。(1)(3)解:(1)(3)