安徽省江南十校高三3月综合素质检测数学(理)答案 安徽省江南十校高三数学3月综合素质检测试卷 理(PDF) 安徽省江南十校高三数学3月综合素质检测试卷 理(PDF)VIP免费

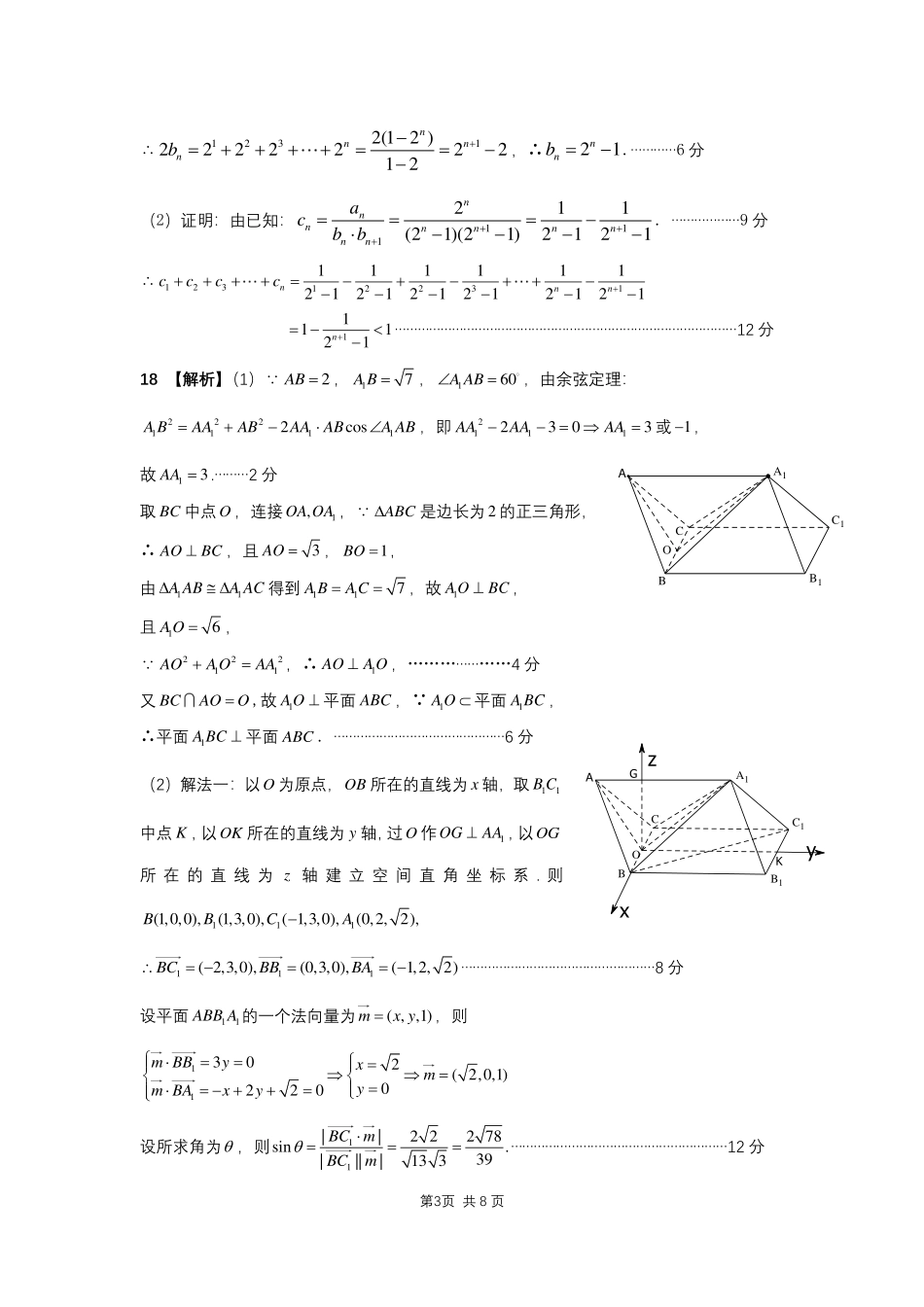
第1页共8页2019安徽省“江南十校”综合素质测试数学（理科）解析及评分标准一、选择题题号123456789101112答案DACBDCCABCBC1.答案D【解析】{2,2}A=−,故选D.2.答案A【解析】|i|12|||||1i|22zz====−,故选A.3.答案C【解析】标准方程为212xy=，故选C.4.答案B【解析】由正弦定理知，sinsin2272cossinsin3BCCCC===，7cos,3C=25cos22cos1,9CC=−=故选B.5.答案Ｄ【解析】12ABAD=，2+3AEABAD=，BDABAD=−+212211(+)()1323326AEBDABADABAD=−+=−+−=−,故选D.6.答案C【解析】11121=2ABCABCVL−三棱柱,故选C7.答案C【解析】由已知得，24=，112,()cos().223fxx==+故选C.8.答案A【解析】由已知得()(),()fxfxyfxR−=−=且在上单调递增，22(3log)(log1)fxfx−由可得223loglog1xx−21log2x−，解得：20.2x故选A.9.答案B【解析】记(1,0)A，则2224||2bcPFa−==，2214||22bcPFaa+=+=，1||1FAc=+，2||1FAc=−，由角平分线性质得21122||||404||||PFFAcccPFFA=−==，或作1ADPF⊥于D,由角平分线的对称性质知1112||||||||||24DFPFPDPFPFa=−=−==，2||||1ADAFc==−，在1RtADF中，222112||1,||||||AFcAFAFAD=+=+,解得4c=故12212214||||24.22PFFcSFFPFc−===故选B.10.答案C【解析】由已知，minmin()()fxgx，由已知可得2min()(1),fxk=+min()3gx=，2(1)3,423,kk+−故选C.第2页共8页11.答案B【解析】由已知得原几何体是由一个棱长为2的正方体挖去一个四分之一圆柱及一个八分之一球体得到的组合体，216245420,484S=−−++=+表故选B.12.答案C【解析】前44组共含有数字：44(441)1980+=个，198044(20191980)2019441975,S=−+−=−=故选C.二、填空题题号13141516答案21−2405713.答案２【解析】0,2xy==时，min3022z=+=14.答案1−【解析】22sincos1sin4cos4=+，2tan14tan4=+，tan2=，123tan=tan()11123−+−==−+.15.答案240【解析】66()=()xyzxyz++++，含2z的项为24226TC()xyz=+，所以形如2abxyz的项的系数之和为246C2=240.16.答案57【解析】由已知动点P落在以AB为轴、底面半径为21的圆柱的侧面上，该侧面与三棱锥侧面ACD的交线为椭圆的一部分，设其与AC的交点为P，此时PB最大，由P到AB的距离为21可得P为AC的中点，且2cos,5BAC=在BAP中，由余弦定理可得22285285575PB=+−=.三、解答题17【解析】（1）由1232nnaaaab++++=①2n时，123112nnaaaab−−++++=②①−②可得：12()nnnabb−=−(2)n，∴3322()8abb=−= 12,0naa=，设{}na公比为q，∴218aq=，∴2q=…………………………3分∴1222nnna−==第3页共8页∴12312(12)222222212nnnnb+−=++++==−−，∴21nnb=−.…………6分（2）证明：由已知：111211(21)(21)2121nnnnnnnnnacbb+++===−−−−−.………………9分∴12312231111111212121212121nnncccc+++++=−+−++−−−−−−−111121n+=−−………………………………………………………………………………12分18【解析】（1） 2AB=，17AB=，160AAB=，由余弦定理：22211112cosABAAABAAABAAB=+−，即21112303AAAAAA−−==或1−，故13AA=.………2分取BC中点O，连接1,OAOA， ABC是边长为2的正三角形，∴AOBC⊥，且3AO=，1BO=，由11AABAAC得到117ABAC==，故1AOBC⊥，且16AO=， 22211AOAOAA+=，∴1AOAO⊥，…………………4分又BCAOO=,故1AO⊥平面ABC， 1AO平面1ABC，∴平面1ABC⊥平面ABC.………………………………………6分（2）解法一：以O为原点，OB所在的直线为x轴，取11BC中点K，以OK所在的直线为y轴，过O作1OGAA⊥，以OG所在的直线为z轴建立空间直角坐标系.则111(1,0,0),(1,3,0),(1,3,0),(0,2,2),BBCA−111(2,3,0),(0,3,0),(1,2,2)BCBBBA=−==−……………………………………………8分设平面11ABBA的一个法向量为(,,1)mxy=，则11302(2,0,1)0220mBByxmymBAxy======−++=设所求角为，则11||22278sin.39||||133BCmBCm===…………………………………………………12分AOA1C1B1BCAGKzyxCOA1C1B1B第4页共8...