导数复习假期作业2014529VIP免费

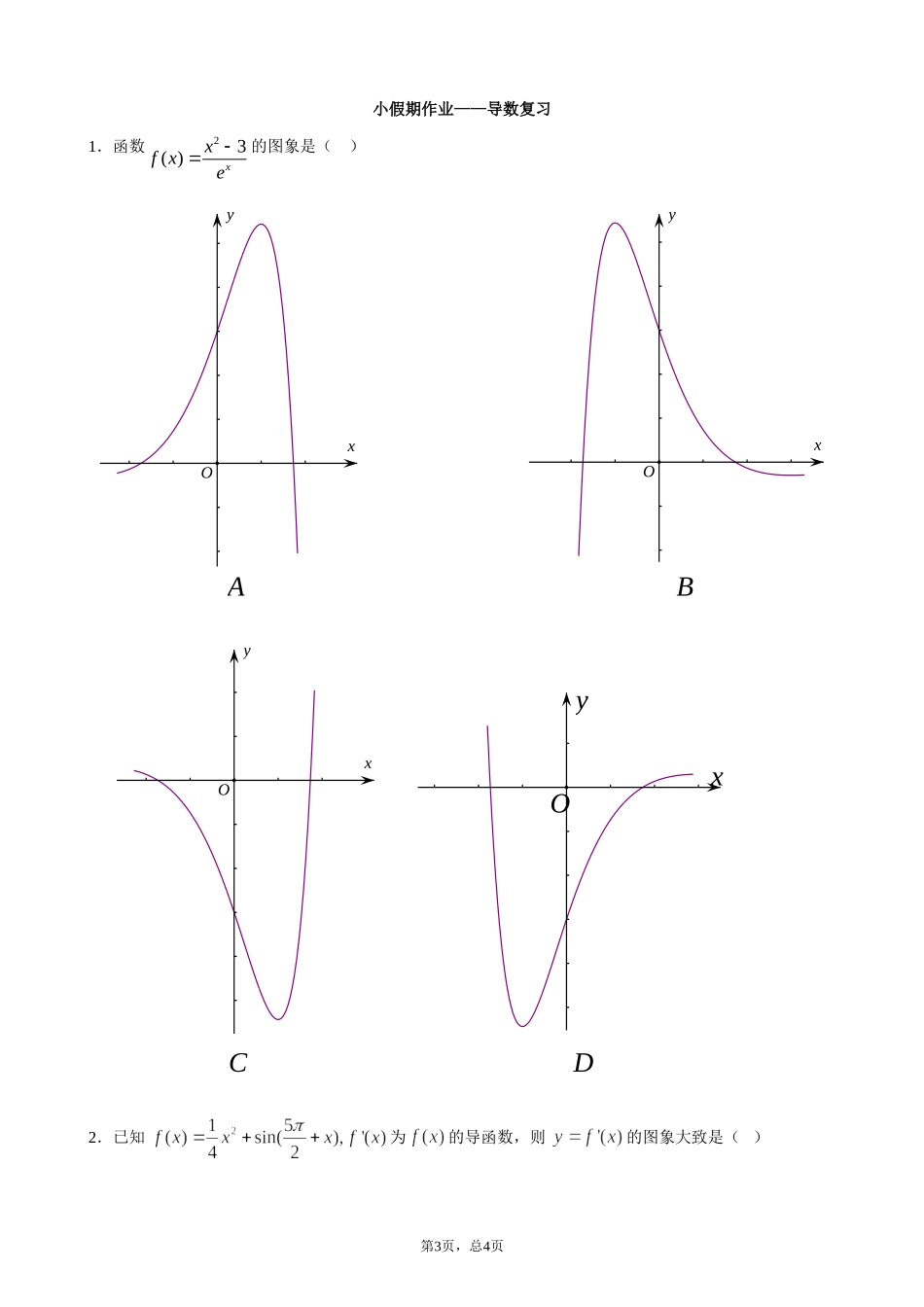
小假期作业——导数复习1．函数23()xxfxe的图象是（）xyAOxyBOxyCOxyDO2．已知为的导函数，则的图象大致是（）第3页，总4页3．函数y=xsinx+cosx在下面哪个区间内是增函数（）A．B．C．D．4．对于上可导的任意函数，若满足，则必有()A.B.C.D.5．函数f(x)的定义域为R，f(－2)=2，对任意xR∈，xf′(x)＞－f(x)，则xf(x)＜－4的解集为（）A．(－2,2)B．（－2，+∞）C．（－∞，－2）D．（－∞，+∞）6．已知函数f(x)Error:Referencesourcenotfound满足f(x)=f()Error:Referencesourcenotfound且当Error:Referencesourcenotfound时,,则（）A.B.C.D.7．设f(x)是定义在R上的奇函数，且f(2)=0,当x>0时，有2()()0xfxfxx恒成立，则不等式2()0xfx的解集是（）(A)(-2,0)(2,+∞)(B)(∪-2,0)(0,2)∪(C)(-∞,-2)(2,+∞)(D)(∪-∞,-2)(0,2)∪8．已知a≤＋lnx对任意x[∈，2]恒成立，则a的最大值为()A．0B．1C．2D．39．(14大连模拟)已知f(x)=alnx+,若对任意两个不等的正实数x1,x2都有>0成立,则实数a的取值范围是()A.[0,+∞)B.(0,+∞)C.(0,1)D.(0,1]10．若f(x)＝－x2＋bln(x＋2)在(－1，＋∞)上是减函数，则b的取值范围是()A．[－1，＋∞)B．(－1，＋∞)C．(－∞，－1]D．(－∞，－1)11．（13湖北）已知函数f（x）=x（lnx﹣ax）有两个极值点，则实数a的取值范围是（）A．（﹣∞，0）B．（0，）C．（0，1）D．（0，+∞）12．已知函数，则使函数有零点的实数的取值范围是（）A．B．C．D．13．已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是()A．∃x0R∈，f(x0)＝0B．函数y＝f(x)的图象是中心对称图形C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)上单调递减D．若x0是f(x)的极值点，则f′(x0)＝0第4页，总4页14．点P是曲线上任意一点，则点P到直线的距离的最小值是15．(14南京模拟)已知曲线f(x)=lnx在点(x0,f(x0))处的切线经过点(0,1),则x0的值为__________.16．若直线2yxm是曲线lnyxx的切线，则实数m的值为．17．已知与的图象在处有相同的切线，则=.18．(14哈尔滨模拟)已知函数f(x)=x2+,g(x)=m.若x1[1,2],∈x2[-1,1]∈使f(x1)≥g(x2),则实数m的取值范围是__________.19．若函数上为递减函数，则m的取值范围是。20．已知函数．若存在实数，，使得的解集恰为，则的取值范围是．21．定义函数（K为给定常数），已知函数，若对于任意的，恒有，则实数K的取值范围为．22．已知，过可作曲线的三条切线，求的取值范围．23．(14郑州模拟)已知函数f(x)=ex+ax,g(x)=ax-lnx,其中a≤0.(1)求f(x)的极值.(2)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.第3页，总4页24．已知函数R）.（1）若曲线在点处的切线与直线平行，求的值；（2）在（1）条件下，求函数的单调区间和极值；（3）当，且时，证明：第4页，总4页25．已知22(),()xxfxxgxxxae.（1）求()()Fxfxx的单调区间和极值；（2）是否存在0x，使得(),()fxgx在0xx的切线相同？若存在，求出0x及(),()fxgx在0xx处的切线；若不存在，请说明理由；（3）若不等式()()fxgx在(0,)x恒成立，求a的取值范围.26．已知函数).(ln)(Raxaxxf(1)若2a，求曲线)(xfy在1x处的切线方程；(2)求)(xf的单调区间；(3）设22)(2xxxg，若对任意),0(1x，均存在]1,0[2x，使得)()(21xgxf，求a的取值范围.第3页，总4页1——5DABCC6——10BDAAC11——13BCC14151617a+b=11819202122（-3，-2）23.（1）f(x)的极小值为f(ln(-a))=-a+aln(-a);没有极大值（2）(-∞,-1)【解析】(1)f(x)的定义域为R,且f′(x)=ex+a.当a=0时,f(x)=ex,故f(x)在R上单调递增.从而f(x)没有极大值,也没有极小值.当a<0时,令f′(x)=0,得x=ln(-a).f(x)和f′(x)的情况如下：x(-∞,ln(-a))ln(-a)(ln(-a),+∞)f′(x)-0+f(x)↘↗故f(x)的单调递减区间为(-∞,ln(-a));单调递增区间为(ln(-a),+∞).从而f(x)的极小值为f(ln(-a))=-a+aln(-a);没有极大值.(2)g(x)的定义域为(0,+∞),且g′(x)=a-Error:Referencesourcenotfound=Error:Referencesourcenotfound.当a=0时,f(x)在R上单调递增,g(x)在(0,+∞)上单调递减,不合题意.当a<0时,g′(x)<0...