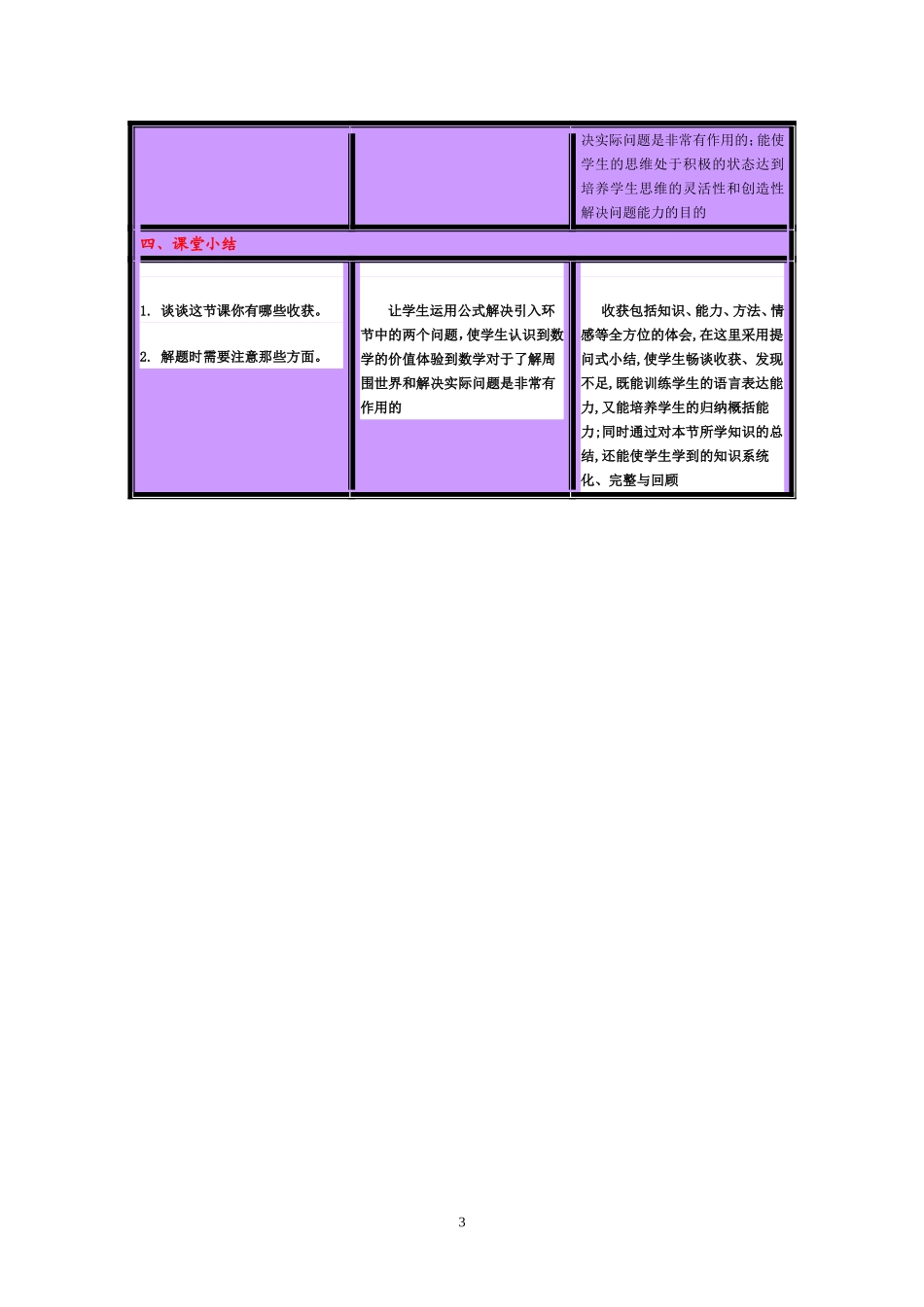
圆柱的体积教师行为学生学习活动设计意图一、情景引入1.出示圆柱形水杯。(1)老师在杯子里面装满水,想一想,水杯里的水是什么形状的?(2)你能用以前学过的方法计算出这些水的体积吗?(3)讨论后汇报:把水倒入长方体容器中,量出数据后再计算。(4)说一说长方体体积的计算公式。2.创设问题情景。如果要求压路机圆柱形前轮的体积,或是求圆柱形柱子的体积,还能用刚才那样的方法吗?刚才的方法不是一种普遍的方法,那么在求圆柱体积的时候,有没有像求长方体或正方体体积那样的计算公式呢?今天,我们就来一起研究圆柱体积的计算方法。(出示课题:圆柱的体积)操作感悟这个环节设计观察活动,意图是让学生通过观察自主得出圆柱体积的定义,进一步加深对体积概念的理解,并为下面的探究活动提供研究方法。二、自主探究1)比较大小、探究圆柱的体积与哪些要素有关。(1)、先出示了两个大小不等的圆柱体让学生判断哪个体积大?(2)、提问:“要比较两个圆柱体的体积你有什么好办法?”学生想到将圆柱体放进水中,比较哪个水面升得高。2)大胆猜想,感知体积公式,确定探究目标。(1)、再次设疑:如果要准确的知道哪个圆柱的体积大,大多少,你有什么好办法?让学生运用这样的方法自己比较底等高不等和高等底不等的两组圆柱的体积,并将实验结果填入实验报告1中。(课件出示)学生通过动手操作汇报结论:当底等时,圆柱越高体积越大;当高等时,圆柱底面越大体积越大。即圆柱的体积的大小与它的底面积和高有关。学生小组讨论交流并汇报:圆柱平均分成若干小扇形体后应该也能够转化成一个近似长方体;圆柱的体积可能也是用底面积乘高来计算。本环节教学让学生根据已有的知识解决简单的问题,通过探究活动,引导学生找出决定圆柱体积的两个因素,为学习新知识作铺垫,同时也发展了学生的抽象概括能力。通过设疑使学生认识到学习圆柱体积公式的必要性,激发学生的探究兴趣。接着通过设计猜想的过程,充分运用学生已有的知识经验,让学生回忆了学习长方体体积时的实践方法和将圆形转化成长方形的过程,学生在如此丰富的知1学生想如何计算圆柱的体积。(2)、引导学生回忆圆的面积公式和长方体的体积公式的推导过程。(3)、让学生思考:怎样计算圆柱的体积呢,依据学过的知识,你可以做出怎样的假设?3)确定方法,探究实验,验证体积公式。(1)、首先要求学生利用实验工具,自主商讨确定研究方法。(2)、学生通过讨论交流确定了两种验证方案。方案一:将圆柱C放入水中,验证圆柱C的体积。方案二:将学具中已分成若干分扇形块的圆柱D拆拼成新的形体,计算新形体的体积,验证圆柱D的体积。(3)、学生按照自己所设想的方案动手实验,并记录有关数据,填入实验报告2中。(课件出示)让学生依据假设结论分组测量圆柱C和圆柱D的有关数据,用计算器计算体积,并填入实验报告2中。(课件出示)实验后让学生对数据进行分析:用实验的方法得出的数据与实验前假想计算的数据进行比较,你发现了什么?学生汇报:实验的结果与猜想的结果基本相同。教师用课件演示将圆柱体转化成长方体的过程,向学生明确圆柱的体积确实可以像计算长方体体积那样,用底面积乘以高。(课件出示)小结:要想求出一个圆柱的体积,需要知道什么条件?学生自学第8页例4上面的一段话:用字母表示公式。学生反馈自学情况v=sh识经验基础上就做到了心中有数,猜想的胆量就更大,假想的合理性就更强。这部分教学采用以小组合作探究的学习方式进行数学活动,充分调动学生各种感官,完成从操作→观察、比较→归纳推理的认知过程,让学生通过自己动手、动脑得到结论。通过让学生自己设计实验方案和自主实验探究的活动,培养了学生的创新精神和实践能力。三、练习提高1.课件出示例4,学生独立完成。指名说说这样列式的依据是什么。2.完成第9页的“试一试”和练一练”中的两道题。3.(“练一练”只列式,不计算)4.集体订正,说一说圆柱体的体积还可以怎样算?让学生在掌握公式的基础上理解公式,学会灵活运用公式的训练题。通过对公式的拓展性理解,可以进一步加深学生对圆柱体积公式的理解和掌握,同时也能培养学生的逻辑思维能力。使学生注意解题格式,...