方程的根与函数的零点VIP免费

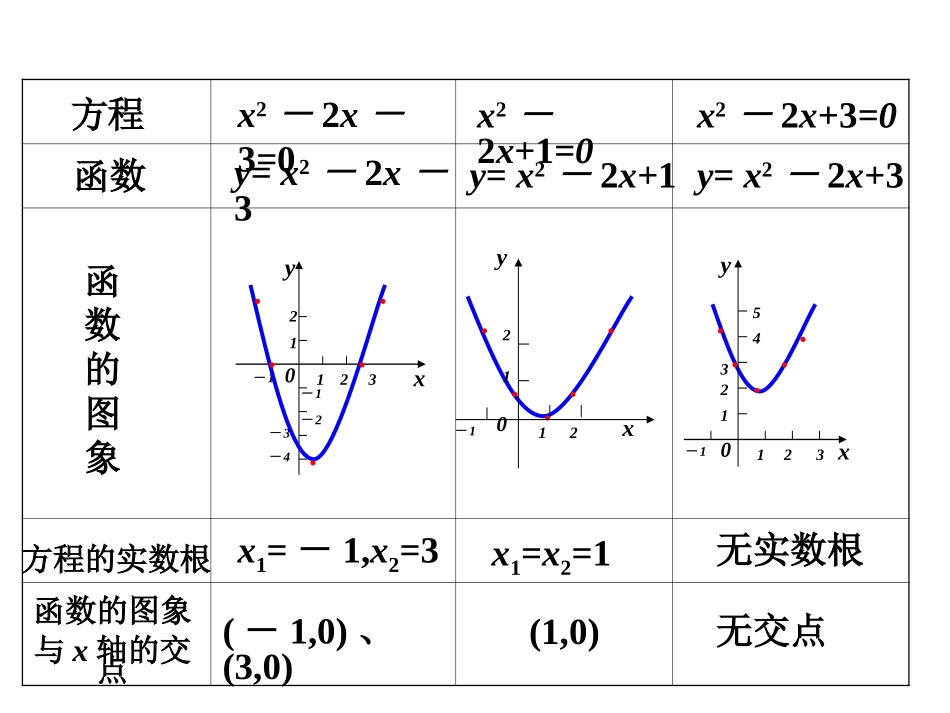
一元二次方程)0(02acbxax的根与二次函数)0(2acbxaxy的图像有什么关系？思考：方程x2－2x+1=0x2－2x+3=0y=x2－2x－3y=x2－2x+1函数函数的图象方程的实数根x1=－1,x2=3x1=x2=1无实数根函数的图象与x轴的交点(－1,0)、(3,0)(1,0)无交点x2－2x－3=0xy0－132112－1－2－3－4..........xy0－132112543.....yx0－12112y=x2－2x+3判别式>00<0y=ax2+bx+c的图象ax2+bx+c=0的根ax2+bx+c>0(a>0)ax2+bx+c<0(a>0)一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有如下关系：xyx1x20xy0x1xy0{x|xx2}{x|x1”或“<”)发现在区间(-2，1)上有零点2.f(2)=，f(4)=f(2)f(4)0(填“>”或“<”)发现在区间(2，4)上有零点观察二次函数f(x)=x2-2x-3图象xy0－132112－1－2－3－4<5-4-1<3-35二、函数零点存在性定理：如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线，并且有f(a)·f(b)<0，那么，函数y=f(x)在区间(a,b)内有零点。即存在c(∈a,b)，使得f(c)=0，这个c也就是方程f(x)=0的根。ababba加强定理的结论:若在区间[a，b]上连续函数f（x）满足f(a)f(b)<0,是否意味着函数f(x)在[a,b]上恰有一个零点?将定理反过来:若连续函数f(x)在[a,b]上有一个零点,是否一定有f(a)f(b)<0?如果函数()yfx在区间,ab上的图象是连续不断的一条曲线，并且有()()0fafb，那么，函数()yfx在区间,ab内有零点，即存在,cab，使得()0fc，这个c也就是方程()0fx的根。三、判断零点的方法：(1)定义法：解方程f(x)=0，得出函数的零点。(2)图象法：画出y=f(x)的图象，其图象与x轴交点的横坐标。(3)定理法：函数零点存在性定理。求下列函数的零点:226)(58log)(442)(334)(21)(122xxxxfxxfxfxxxfxxfx1)1(x31)2(xx2)3(x82)4(x6)5(x例1:方程在下列哪个区间上有零点()A.(0,1)B.(1,2)C.(2,3)D.(3,4)032024ln403ln3022ln241ffffff062lnxxC解法一:C解法二:62lnxx62lnxxgxxf21-1-21240yx3例1:方程在下列哪个区间上有零点()A.(0,1)B.(1,2)C.(2,3)D.(3,4)062lnxx0x练习1:下列函数在区间[1，2]上有零点的是()(A)f(x)=3x2-4x+5(B)f(x)=x³-5x-5(C)f(x)=lnx-3x+6(D)f(x)=ex+3x-6练习2:f(x)=x3+x-1在下列哪个区间上有零点()A.(-2,-1)B.(0,1)C.(1,2)D.(2,3)DB1、对于定义在R上的连续函数y=f(x),若f(a).f(b)<0(a,b∈R,且a–2Bm<–2Cm>2Dm<2BB【课堂总结】一元二次方程的根及其相应二次函数的图象与x轴交点的关系;函数零点的概念;函数零点与方程的根的关系.