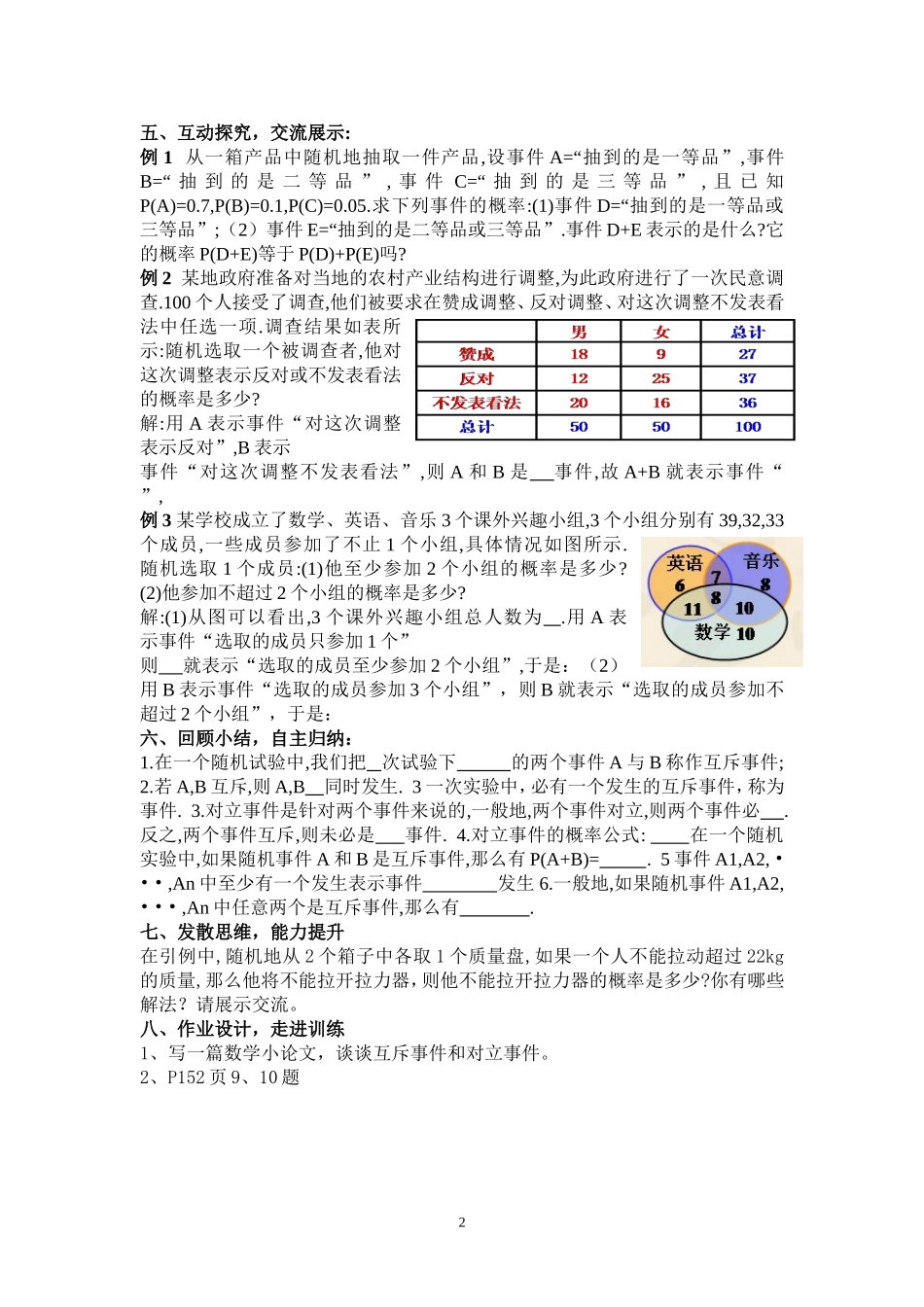
互斥事件(1)教案设计陇县第二高级中学高一数学组戚武智【教学目标】知识与技能:1.理解互斥事件和对立事件的概念,能正确分辨互斥事件和对立事件。2.理解互斥事件和对立事件的计算公式.过程与方法:通过互斥事件和对立事件计算公式的形成过程探究,培养学生的分析问题和探究问题的能力,体会归纳过程,掌握对生活问题分析和处理的方式和方法.情感态度价值观:通过概念的形成过程、公式的发现过程渗透归纳思想,优化思维品质,体会“分析——探究——归纳——应用”,学会学习,学会交流。【教学重点】:互斥事件和对立事件的概念、公式、应用.【教学难点】:实际问题的分析与转化、求解。【教学方法】问题互动探究法引导发现法【学法指导】:合作——交流——互助——探究【教学手段】通过多媒体和学案辅助教学【教学过程】一、问题提出,引入新课一袋中装有2个红球,3个黄球,5个白球,各球除了颜色外其他都相同,从中任意摸出一球,设A=“摸出红球”,B=“摸出黄球”,C=“摸出白球”,D=“摸出的球不是白球”.回答下列问题:(1)求这些事件发生的概率P(A),P(B),P(C),P(D);(2)摸出红球或黄球的概率是多少?(3)C与D能同时发生吗?A与B呢?二、揭示概念,比较辨析1.互斥事件:在一个随机试验中,我们把一次试验下不能同时发生的两个事件A与B称作互斥事件.(提问:两个以上的事件能否是互斥事件?)2.对立事件:一次实验中,必有一个发生的互斥事件,称为对立事件.3.回归课本,概念辨析.三、典例回顾,探究新知:在典型例题中,随机地从2个箱子中各取1个质量盘,下面的事件A和B是否是互斥事件?(1)事件A=“总质量为20kg”,事件B=“总质量为30kg”;(2)事件A=“总质量为7.5kg”,事件B=“总质量超过10kg”;(3)事件A=“总质量不超过10kg”,事件B=“总质量超过10kg”;(4)事件A=“总质量为20kg”,事件B=“总质量超过10kg”.对例3的(1),(2)和(3)中的每一对事件,通过计算完成下表:你发现P(A+B)与P(A)+P(B)有什么样的大小关系?四、小组互助,交流探究:在一个随机实验中,如果随机事件A和B是互斥事件,那么有P(A+B)=P(A)+P(B).1五、互动探究,交流展示:例1从一箱产品中随机地抽取一件产品,设事件A=“抽到的是一等品”,事件B=“抽到的是二等品”,事件C=“抽到的是三等品”,且已知P(A)=0.7,P(B)=0.1,P(C)=0.05.求下列事件的概率:(1)事件D=“抽到的是一等品或三等品”;(2)事件E=“抽到的是二等品或三等品”.事件D+E表示的是什么?它的概率P(D+E)等于P(D)+P(E)吗?例2某地政府准备对当地的农村产业结构进行调整,为此政府进行了一次民意调查.100个人接受了调查,他们被要求在赞成调整、反对调整、对这次调整不发表看法中任选一项.调查结果如表所示:随机选取一个被调查者,他对这次调整表示反对或不发表看法的概率是多少?解:用A表示事件“对这次调整表示反对”,B表示事件“对这次调整不发表看法”,则A和B是事件,故A+B就表示事件“”,例3某学校成立了数学、英语、音乐3个课外兴趣小组,3个小组分别有39,32,33个成员,一些成员参加了不止1个小组,具体情况如图所示.随机选取1个成员:(1)他至少参加2个小组的概率是多少?(2)他参加不超过2个小组的概率是多少?解:(1)从图可以看出,3个课外兴趣小组总人数为.用A表示事件“选取的成员只参加1个”则就表示“选取的成员至少参加2个小组”,于是:(2)用B表示事件“选取的成员参加3个小组”,则B就表示“选取的成员参加不超过2个小组”,于是:六、回顾小结,自主归纳:1.在一个随机试验中,我们把次试验下的两个事件A与B称作互斥事件;2.若A,B互斥,则A,B同时发生.3一次实验中,必有一个发生的互斥事件,称为事件.3.对立事件是针对两个事件来说的,一般地,两个事件对立,则两个事件必.反之,两个事件互斥,则未必是事件.4.对立事件的概率公式:在一个随机实验中,如果随机事件A和B是互斥事件,那么有P(A+B)=.5事件A1,A2,•••,An中至少有一个发生表示事件发生6.一般地,如果随机事件A1,A2,•••,An中任意两个是互斥事件,那么有.七、发散思维,能力提升在引例中,随机地从2个箱子中各取1个质量盘,如果一个人不能拉动超过22kg的质量,那么他将不能拉开拉力器,则他不能拉开拉力器的概率是多少?你有哪些解法?请展示交流。八、作业设计,走进训练1、写一篇数学小论文,谈谈互斥事件和对立事件。2、P152页9、10题2