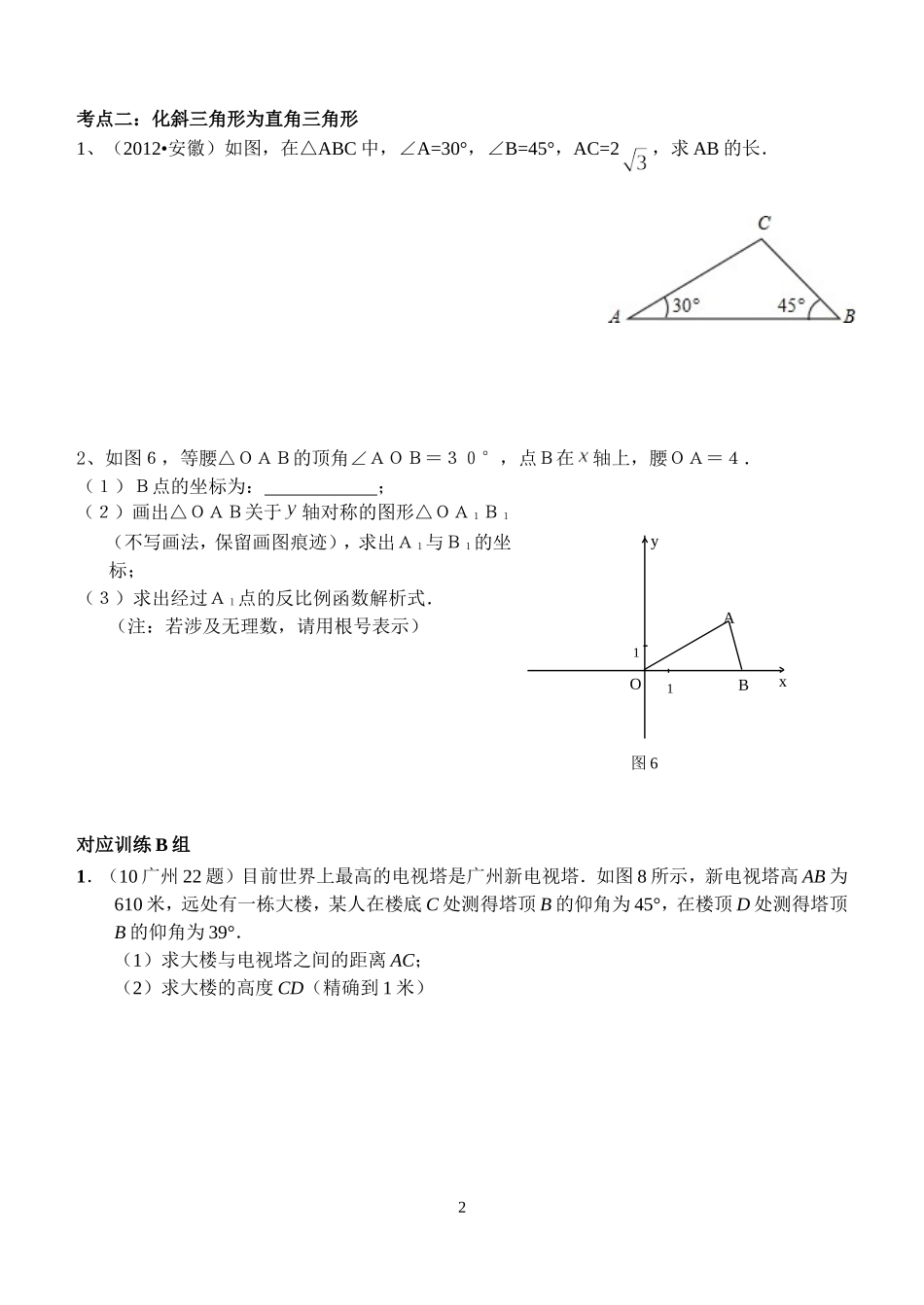
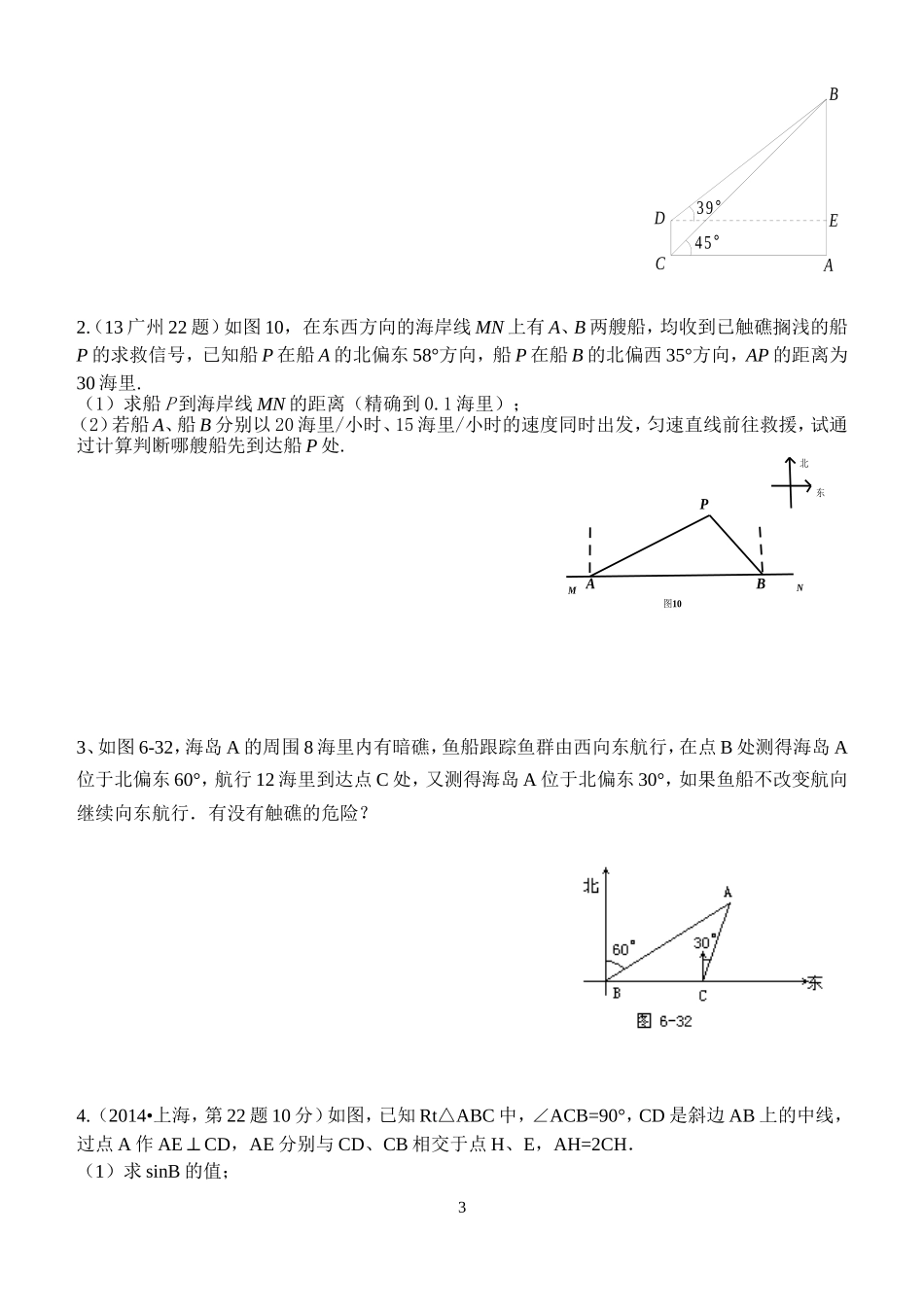
2015年初三数学第二轮专题复习六解直角三角形对应会考指导书第五章之解直角三角形班级____________姓名___________1、定义:由直角三角形中除直角外的个已知元素,求出另外个未知元素的过程叫解直角三角形2、解直角三角形的依据Rt∠ABC中,∠C=900三边分别为a、b、c⑴三边关系:⑵两锐角关系提醒:解直角三角形中已知的两个元素应至少有一个是3、斜坡AB的垂直高度H和水平宽度L的比叫做坡度,用i表示,即i=坡面与水平面得夹角为用字母α表示,则i==4、俯角、仰角、方位角A组考点一:锐角三角函数的概念例1(2012•内江)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()A.B.C.D.思路分析:利用网格构造直角三角形,根据锐角三角函数的定义解答.对应训练1.(2012•贵港)在平面直角坐标系中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于()A.B.C.D.2、(2014•宁夏,第20题6分)在△ABC中,AD是BC边上的高,∠C=45°,sinB=,AD=1.求BC的长.(+1)1考点二:化斜三角形为直角三角形1、(2012•安徽)如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求AB的长.2、如图6,等腰△OAB的顶角∠AOB=30°,点B在轴上,腰OA=4.(1)B点的坐标为:;(2)画出△OAB关于轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;(3)求出经过A1点的反比例函数解析式.(注:若涉及无理数,请用根号表示)对应训练B组1.(10广州22题)目前世界上最高的电视塔是广州新电视塔.如图8所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(1)求大楼与电视塔之间的距离AC;(2)求大楼的高度CD(精确到1米)2y1x1O图6BA45°39°DCAEB2.(13广州22题)如图10,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.(1)求船P到海岸线MN的距离(精确到0.1海里);(2)若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.3、如图6-32,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛A位于北偏东30°,如果鱼船不改变航向继续向东航行.有没有触礁的危险?4.(2014•上海,第22题10分)如图,已知RtABC△中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.(1)求sinB的值;3PBA图10北东NM(2)如果CD=,求BE的值.考点:解直角三角形;直角三角形斜边上的中线.分析:(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=BCD∠,再由AECD⊥,可证明∠B=CAH∠,由AH=2CH,可得出CH:AC=1:,即可得出sinB的值;(2)根据sinB的值,可得出AC:AB=1:,再由AB=2,得AC=2,则CE=1,从而得出BE.解答:解:(1) ∠ACB=90°,CD是斜边AB上的中线,CD=BD∴,B=BCD∴∠∠,AECD ⊥,CAH+ACH=90°∴∠∠,B=CAH∴∠∠,AH=2CH ,∴由勾股定理得AC=CH,CH∴:AC=1:,sinB∴;(2) sinB,AC∴:AB=1:,CD= ,AB=2∴,由勾股定理得AC=2,则CE=1,在RtABC△中,AC2+BC2=AB2,BC=4∴,BE=BCCE=3∴﹣.点评:本题考查了解直角三角形,以及直角三角形斜边上的中线,注意性质的应用,难度不大.4C组1.(11广州23题)已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y=的图象上,且sin∠BAC=。(1)求k的值和边AC的长;(2)求点B的坐标。2.(2014•株洲,第22题,8分)如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).(1)求证:△ACE≌△AFE;(2)求tan∠CAE的值.考点:全等三角形的判定与性质;角平分线的性质;勾股定理;锐角三角函数的定义分析:(1)根据角的平分线的性质可求得CE=EF,然后根据直角三角形的判定定理求得三角形全等.(2)由△ACE≌△AFE,得出AC=AF,CE=EF,设BF=m,则AC...