第9讲梯度法和共轭梯度法VIP免费

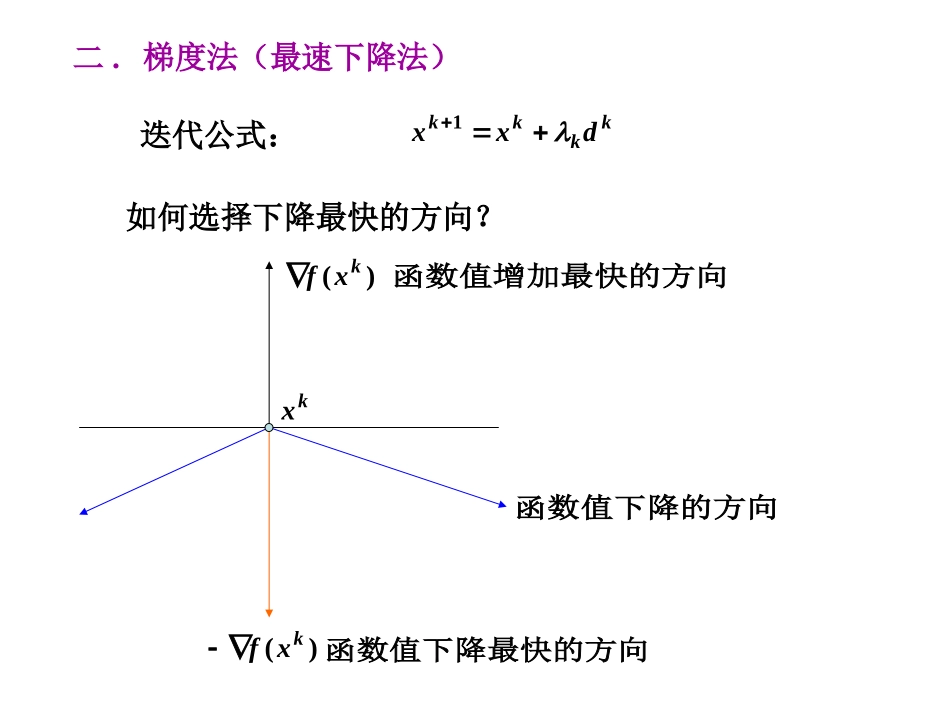
4.1梯度法和共轭梯度法1.无约束最优化问题2.梯度法3.共轭梯度法一.无约束最优化问题无约束最优化问题nRxtsxf..)(min有一阶连续偏导数。其中)(xf解析方法：利用函数的解析性质构造迭代公式使之收敛到最优解。二.梯度法（最速下降法）迭代公式：kkkkdxx1如何选择下降最快的方向？)(kxf)(kxf函数值下降最快的方向函数值增加最快的方向函数值下降的方向kx梯度法（最速下降法）：也称为最速下降方向；搜索方向：,)(.1kkxfd。即满足取最优步长搜索步长)(min)(,:.2kkkkkkdxfdxf梯度法算法步骤：。令允许误差给定初始点1,0,.11kRxn;)(.2kkxfd计算搜索方向kkkxd否则，求最优步长为所求极值点；则停止计算，若,||||.3。使得)(min)(kkkkkdxfdxf。转令令2,1:,.41kkdxxkkkk,)1,2(,3)(min:.12221Txxxxf设初始点为用最速下降法求解例。求迭代一次后的迭代点2x解：,)6,2()(21Txxxf.)6,4()(11Txfd.)61,42(11Tdx，令2211)61(3)42()()(dxf)(min求解0)61(36)42(8)(令62131Tdxx)318,3136(1112收敛性)(min)(kkkkkdxfdxf。则有0)(kTkkkddxf性质.证明：所以，令)()(kkdxf.)()(kTkkddxf)(min)(kkkkkdxfdxf.0)()(kTkkkkddxf满足步长有一阶连续偏导数，若设kxf)(注：。kkkTkdddd110)(所以，因为梯度法的搜索方向)(1kkkkdxfd锯齿现象在极小点附近，目标函数可以用二次函数近似，其等值面近似椭球面。1x*x2x3x它只是。标函数的一种局部性质最速下降方向反映了目局部目标函数值下降最快的方向。锯齿形状,越接近极小点,步长越小,前进越慢!注最速下降法反映的目标函数的一种局部性质,从局部看,最速下降方向确是目标函数值下降最快的方向,选择这样的方向进行搜索是有利的.但从全局来看,由于锯齿现象的影响,即使向着极小点移近不太大的距离,也要经历不小的”弯路”,因此收敛速度大为减慢.最速下降法一般适用于计算过程的前期迭代,或者作为间插步骤.最速下降法产生的序列是线性收敛的,而且其收敛性质与极小点处的Hesse矩阵2()fx特征值有关.定理1设()fx存在连续二阶偏导数,x是局部极小点,Hesse矩阵2()fx的最小特征值0a,最大特征值为A.算法产生的序列kx收敛于x,则目标函数值的序列()kfx以不大于2AaAa的收敛比线性的收敛于()fx.若令/rAa,则22111AarAar.r称为对称正定矩阵2()fx的条件数(conditionnumber).定理表明：条件数越小,收敛越快;条件数越大,收敛越慢!叁.共轭梯度法1.共轭方向和共轭方向法定义共轭。关于和，则称若有AddAddT21210ARdddnk它们两两关于中一组非零向量，如果是设,,,21。共轭，即kjijiAddjTi,,2,1,,,0共轭方向。组共轭的，也称它们是一则称这组方向是关于AA注：002121dddIdTT21dd共轭是正交的推广。，和中的两个非零向量的对称正定矩阵，对于是设21ddRnnAn是单位矩阵，则如果A共轭的非零个是阶对称正定矩阵，是设AkdddnAk,,,21性无关。向量，则这个向量组线2.定理证明，使得设存在实数k,,,21,01kiiidjTdA上式两边同时左乘，则有,01kiiTjiAdd可化简为共轭的向量，所以上式个是因为Akdddk,,,21.0jTjjAdd0,0jjTjdAdAd因为而是正定矩阵，所以，所以。kjj,,2,1,0线性无关。因此kddd,,,21几何意义设有二次函数)()(21)(xxAxxxfT对称正定矩阵，是其中nnA是一个定点。x的等值面则函数)(xfcxxAxxT)()(21为中心的椭球面。是以x由于,0)()(xxAxf,0)(2AxfA所以正定，因为的极小点。是因此)(xfxx,)(2Axf而点，是在某个等值面上的一设)0(x处的法向量为该等值面在点)1(x.)()()1()1(xxAxfo1x2xx)1(d)0(x中的一个方向，是nRd)1(。以最优步长搜索得到点沿着)1()1()0(xdx所在等值面的切向量。是点则)1()1(xd...