两条直线的交点坐标VIP免费

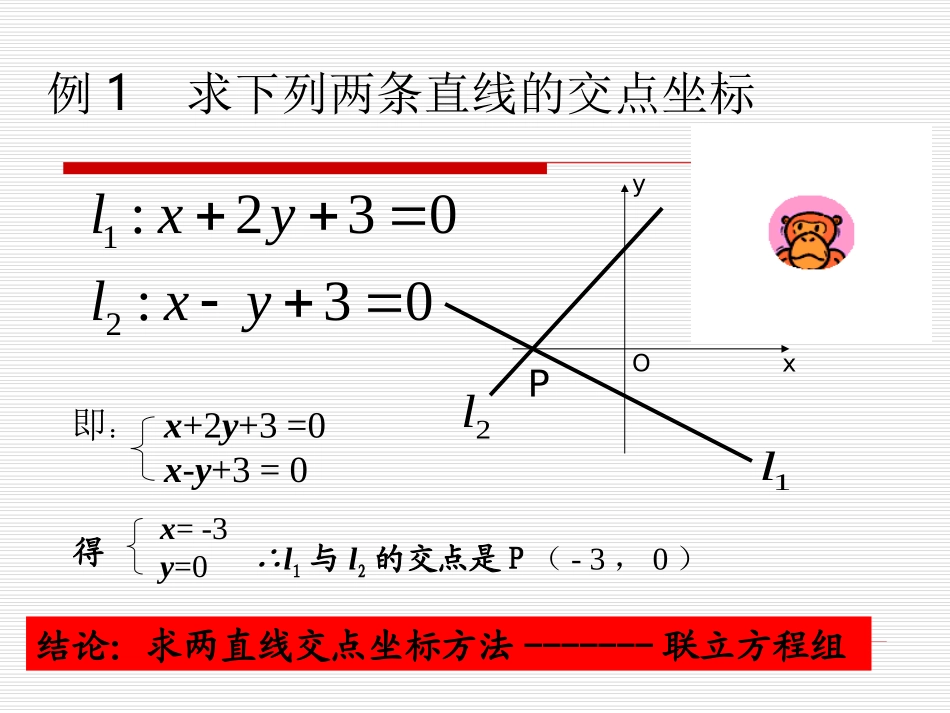
判断下列两条直线的位置关系121:30;:60xxlyly122:30;:302lylyxx问题1：当直线相交时，交点个数有几个？问题2：如何求两相交直线的交点坐标？3.3.1两条直线的交点坐标结论：求两直线交点坐标方法-------联立方程组例1求下列两条直线的交点坐标12:30:230xxlylyxyOx+2y+3=0x-y+3=0即：x=-3y=0得∴l1与l2的交点是P（-3，0）1l2lP练习1：求下列各对直线的交点坐标1212121:3420,:220;22:640,:;3353:3100,:2lxylxyxlxylyxlxyly例2判断下列直线的位置关系。若相交，求出交点坐标。21:20:280lxylxy4,2答案：练习2：判断下列的位置关系。若相交，求出交点坐标。（1）l1:x-y=0,l2:3x+3y-10=0;（2）l1:3x-y+4=0,l2:6x-2y-1=0;（3）l1:3x+4y-5=0,l2:6x+8y-10=0;解:（１）两直线有交点，交点坐标为（２）方程组无解，两直线无交点。（３）两方程可化成同一方程，两直线有无数个交点。l1与l2重合55,3312//ll结论：二元一次方程组的解与两条直线的位置关系无穷多解无穷多解无解无解唯一解唯一解11122200AxByCAxByC121212,,,llllll相交重合平行12:3420:220lxylxy问题3：1224222xyxy交点，，是否满足3+=0？2,2P交点：12220ll也就是说，交点，满足由练习1（1）可知12:3420:220lxylxy问题3：2224222xyxy交点，，是否满足3+0=0？2,2P交点：122200ll也就是说，交点，满足12:3420:220lxylxy问题3：32242122xyxy交点，，是否满足3=0？2,2P交点：122210ll也就是说，交点，满足12:3420:220lxylxy问题3：4224222xyxyR交点，，是否满足3+=0？2,2P交点：12220llR也就是说，交点，满足4222xyxyR方程3+=0所表示的直线有何特点？R思考：当取不同的值时，1340xy当时，直线为：0420xy当时，直线为：310xy当时，直线为：xyOP4222420220xyxyRxyxy结论：方程3+=0所表示的直线恒过3和的交点。2,2P交点：12:3420:220lxylxy12121llRll=0恒过与的交点由此可以得出：1212220llRlll就表示过与的交点的所有直线不含本身2、过交点的直线系方程例3已知直线,证明:直线恒过定点。:31lykxkl是过直线和的交点的直线系方程(不含直线)。1112220AxByCAxByCR1110AxByC2220AxByC2220AxByC证明：将方程变形为130ykx由得1030yx31xy所以直线恒过定点（-3，1）练习4：已知直线，求证：无论为何值时，直线恒过第一象限。:5530laxyala13,55练习3：已知直线恒过一定点，求该点坐标。:2340lmxmy44,551.1.两直线交点的求法两直线交点的求法------联立方程组。联立方程组。2.2.过交点直线系方程及其应用过交点直线系方程及其应用11、、PP109109习题习题3.313.3122、课堂新坐标、课堂新坐标PP979733、能力提升、能力提升已知直线,求证：无论为何值时，直线恒过第一象限。:5530laxyala