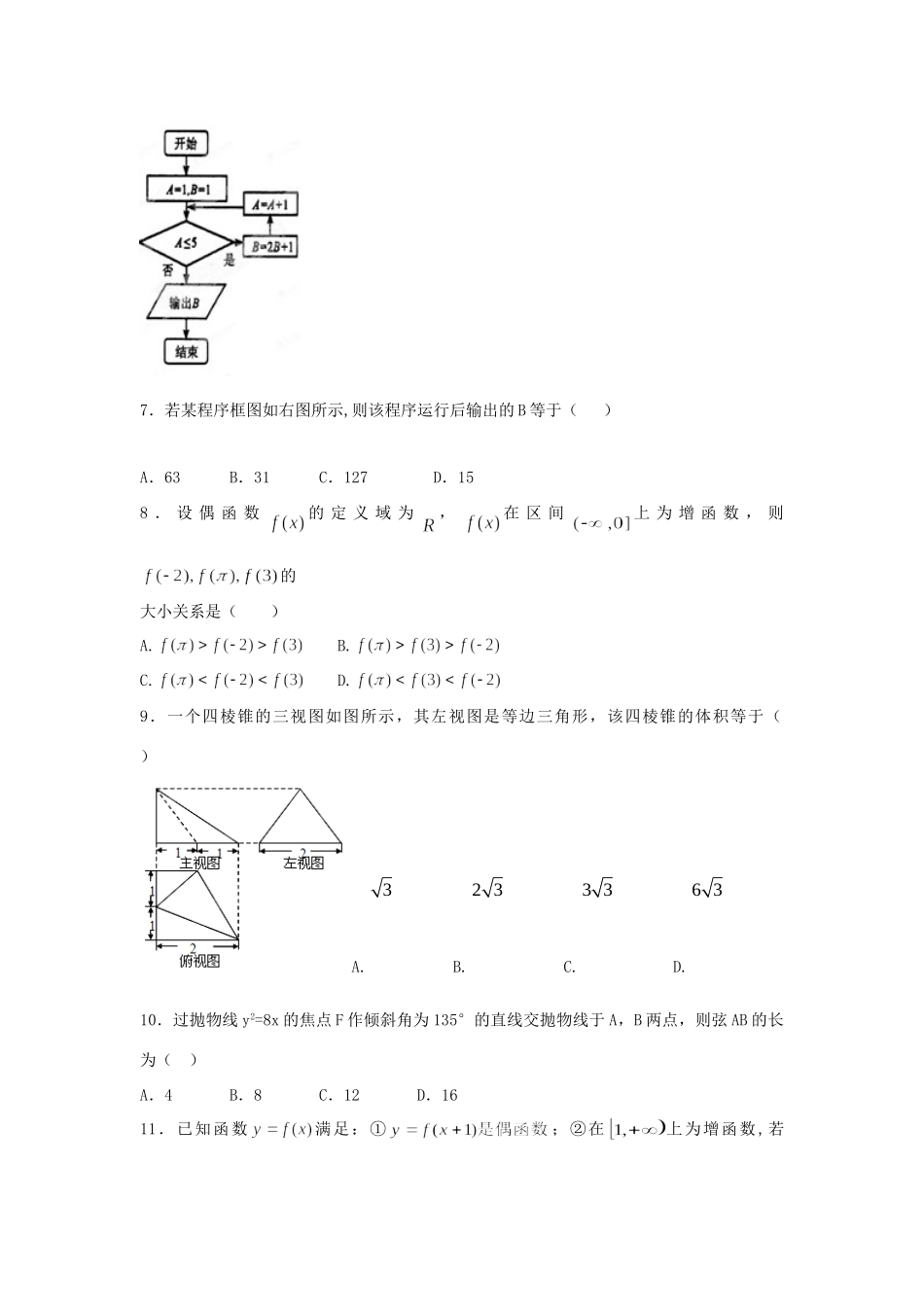
高二理数17年暑期作业51.设全集UR,集合,集合,则()A.|12xxB.C.D.|12xx2.已知集合,则()A.B.C.D.3.若实数满足不等式,且目标函数的最大值为()A.1B.2C.3D.44.在锐角△中,角所对应的边分别为,若,则角等于()A.B.C.D.5.设椭圆C:(a>b>0)的左右焦点分别为F1,F2,过F2作x轴的垂线与C相交于A,B两点,F1B与y轴相交于点D.若AD⊥F1B,则椭圆C的离心率等于()A.B.C.D.6.若cos212sin()4,则sin2的值为()A、78B、78C、47D、477.若某程序框图如右图所示,则该程序运行后输出的B等于()A.63B.31C.127D.158.设偶函数的定义域为,在区间上为增函数,则的大小关系是()A.B.C.D.9.一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积等于()A.3B.23C.33D.6310.过抛物线y2=8x的焦点F作倾斜角为135°的直线交抛物线于A,B两点,则弦AB的长为()A.4B.8C.12D.1611.已知函数满足:①;②在上为增函数,若,且,则与的大小关系是()A.B.C.D.无法确定12.已知函数,若,则实数的取值范围是()A.B.C.D.13.在五个数字1,2,3,4,5中,若随机取出三个数字,则剩下两个数字都是奇数的概率是_________14.已知△ABC中,,,,,,则夹角的余弦值为___.15.已知下列五个命题:①若一个圆锥的底面半径缩小到原来的,其体积缩小到原来的;②若两组数据的中位数相等,则它们的平均数也相等;③直线与圆相切;④“”是“”的充分不必要条件.⑤过M(2,0)的直线l与椭圆交于P1P2两点,线段P1P2中点为P,设直线l的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2等于-。其中真命题的序号是:____.16.将函数220sin,xxf图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移的单位长度得到的图像,则____________.17.已知数列na是公比不为1的等比数列,11a,且231,,aaa成等差数列.(1)求数列na的通项;(2)若数列na的前n项和为nS,试求nS的最大值.18.如图,在四棱锥中,,90ABCBCDCDA,63,6ACBCCD.(1)求证;(2)设点在棱上,且,试求三棱锥E—GCD的体积.19.某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.(1)问各班被抽取的学生人数各为多少人?(2)求平均成绩;(3)在抽取的所有学生中,任取一名学生,求分数不小于90分的概率.20.已知圆:.(Ⅰ)直线过点,且与圆交于、两点,若,求直线的方程;(Ⅱ)过圆上一动点作平行于轴的直线,设与轴的交点为,若向量,求动点的轨迹方程,并说明此轨迹是什么曲线.21.已知(为常数),曲线在点处的切线与直线垂直.(Ⅰ)求的值及函数的单调区间;(Ⅱ)证明:当时,2xex;(Ⅲ)设,若在上单调递减,求实数的取值范围.22.已知曲线的参数方程为(为参数),在同一平面直角坐标系中,将曲线上的点按坐标变换得到曲线.(1)求曲线的普通方程;(2)若点在曲线上,点,当点在曲线上运动时,求中点的轨迹方程.