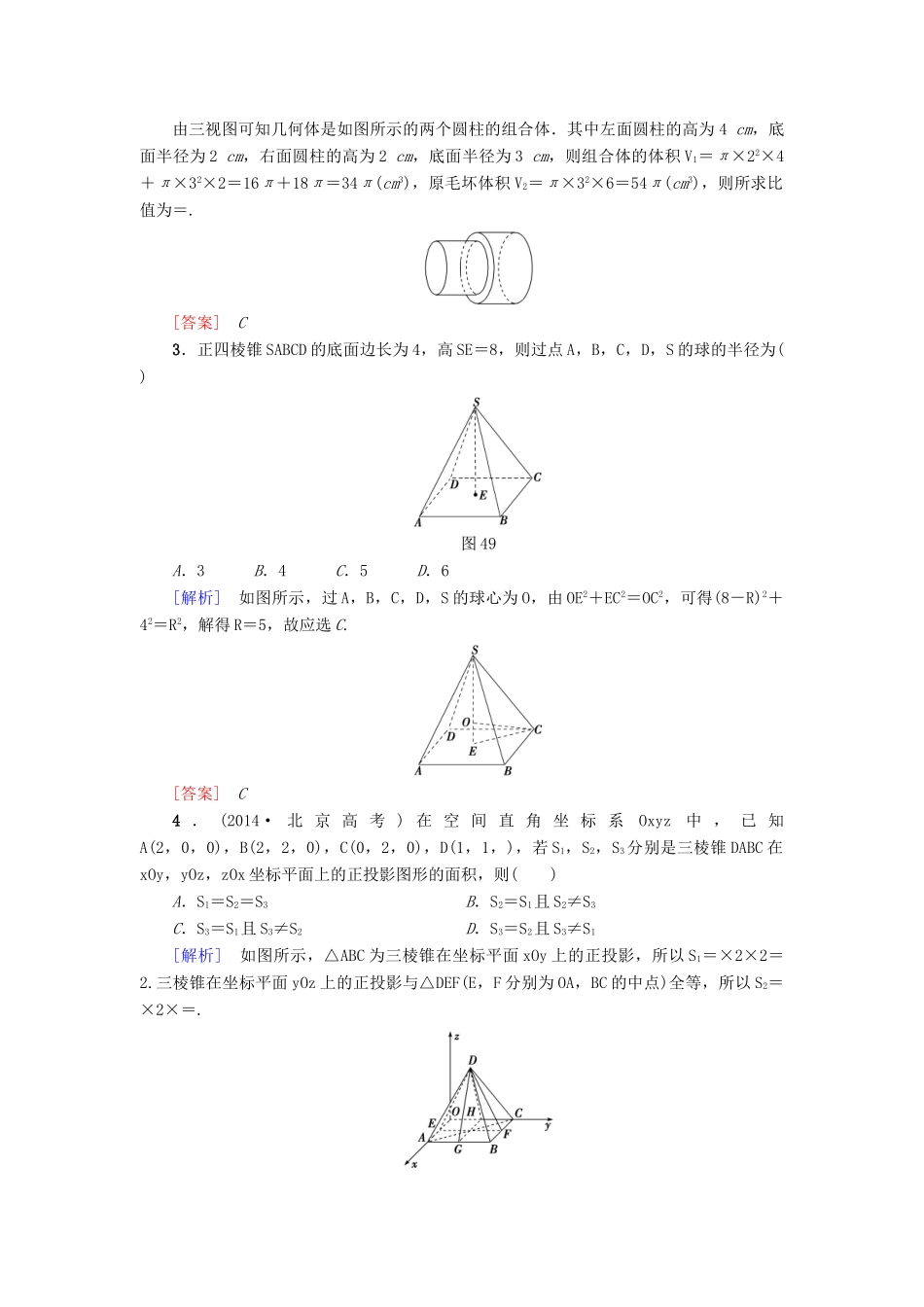
【高考新坐标】2016届高考数学总复习专题突破练四立体几何问题的求解策略[A级基础达标练]一、选择题1.(2015·潍坊质检)将直三棱柱截去三个角(如图47(1)所示,A,B,C分别是△GHI三边的中点)得到的几何体(如图(2)),则该几何体按图(2)所示方向的侧视图(或称左视图)为()(1)(2)图47[解析]当直三棱柱没有截去三个角时,侧视图如图①所示,由此可知截去三个角后的侧视图如图②所示,故选A.①②[答案]A2.(2014·课标全国卷Ⅱ)如图48,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()图48A.B.C.D.[解析]由三视图可知几何体是如图所示的两个圆柱的组合体.其中左面圆柱的高为4cm,底面半径为2cm,右面圆柱的高为2cm,底面半径为3cm,则组合体的体积V1=π×22×4+π×32×2=16π+18π=34π(cm3),原毛坏体积V2=π×32×6=54π(cm3),则所求比值为=.[答案]C3.正四棱锥SABCD的底面边长为4,高SE=8,则过点A,B,C,D,S的球的半径为()图49A.3B.4C.5D.6[解析]如图所示,过A,B,C,D,S的球心为O,由OE2+EC2=OC2,可得(8-R)2+42=R2,解得R=5,故应选C.[答案]C4.(2014·北京高考)在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,),若S1,S2,S3分别是三棱锥DABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则()A.S1=S2=S3B.S2=S1且S2≠S3C.S3=S1且S3≠S2D.S3=S2且S3≠S1[解析]如图所示,△ABC为三棱锥在坐标平面xOy上的正投影,所以S1=×2×2=2.三棱锥在坐标平面yOz上的正投影与△DEF(E,F分别为OA,BC的中点)全等,所以S2=×2×=.三棱锥在坐标平面xOz上的正投影与△DGH(G,H分别为AB,OC的中点)全等,所以S3=×2×=.所以S2=S3且S1≠S3.故选D.[答案]D5.如图410所示,ABCDA1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成二面角的余弦值为()图410A.B.C.D.[解析]以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,易知当E(6,3,0),F(3,6,0)时,A1,E,F、C1共面,设平面A1DE的法向量为n1=(a,b,c),依题意得可取n1=(-1,2,1),同理可得平面C1DF的一个法向量为n2=(2,-1,1),故平面A1DE与平面C1DF所成二面角的余弦值为=.[答案]B二、填空题6.(2013·湖北高考)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是________寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)[解析]圆台的轴截面是下底长为12寸,上底长为28寸,高为18寸的等腰梯形,雨水线恰为中位线,故雨水线直径是20寸,∴降水量为=3(寸).[答案]37.设m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:①若α∥β,m⊂β,n⊂α,则m∥n;②若α∥β,m⊥β,n∥α,则m⊥n;③若α⊥β,m⊥α,n∥β,则m∥n;④若α⊥β,m⊥α,n⊥β,则m⊥n.上面命题中,所有真命题的序号为________.[解析]对于①,m,n可能是异面直线,故①错;对于③,两条直线m和n也可以相交或异面,故③错;②,④正确.[答案]②④8.直三棱柱ABCA1B1C1的各顶点都在同一球面上.若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于________.[解析]设球心为O,球半径为R,△ABC的外心是M,则O在底面ABC上的射影是点M,在△ABC中,AB=AC=2,∠BAC=120°,∠ABC=(180°-120°)=30°,AM==2.因此,R2=22+=5,S球=4πR2=20π.[答案]20π三、解答题9.(2014·湖北高考)如图411,在正方体ABCDA1B1C1D1中,E,F,P,Q,M,N分别是棱AB,AD,DD1,BB1,A1B1,A1D1的中点.求证:图411(1)直线BC1∥平面EFPQ;(2)直线AC1⊥平面PQMN.[证明](1)连结AD1,由ABCDA1B1C1D1是正方体,知AD1∥BC1,因为F,P分别是AD,DD1的中点,所以FP∥AD1.从而BC1∥FP.而FP⊂平面EFPQ,...