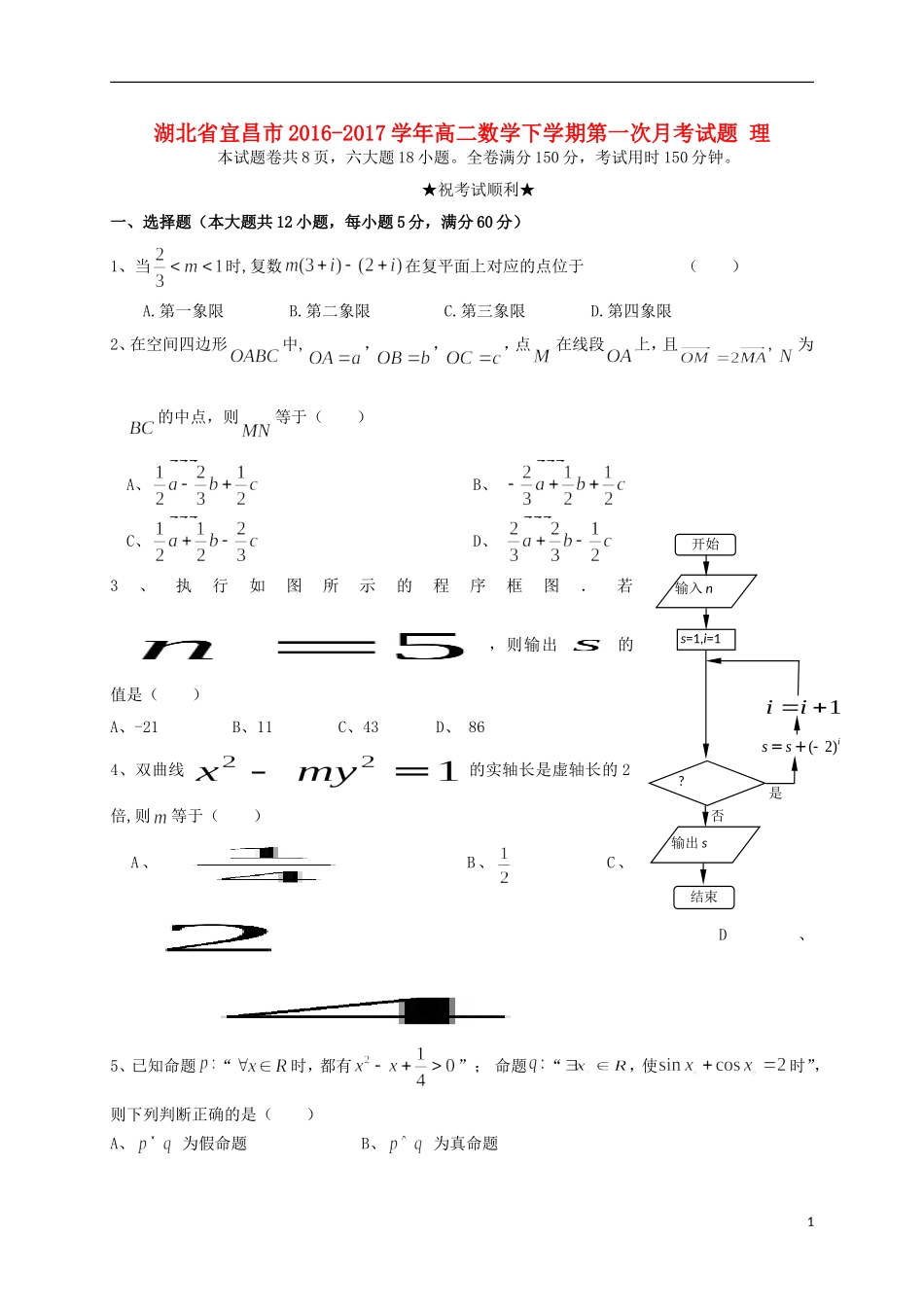
是否结束开始s=1,i=1(2)iss=+-1ii输入n输出s?湖北省宜昌市2016-2017学年高二数学下学期第一次月考试题理本试题卷共8页,六大题18小题。全卷满分150分,考试用时150分钟。★祝考试顺利★一、选择题(本大题共12小题,每小题5分,满分60分)1、当时,复数在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2、在空间四边形中,,,,点在线段上,且,为的中点,则等于()A、B、C、D、3、执行如图所示的程序框图.若,则输出的值是()A、-21B、11C、43D、864、双曲线的实轴长是虚轴长的2倍,则等于()A、B、C、D、5、已知命题“时,都有”;命题“,使时”,则下列判断正确的是()A、为假命题B、为真命题1C、为真命题D、为假命题第3题6、已知m,n表示两条不同直线,表示平面,下列说法正确的是()A.若则B.若,,则C.若,,则D.若,,则7、若实数满足,则关于的方程有实数根的概率是()A、B、C、D、8、设,则的展开式中各项系数和为()A.1B.2C.3D.49、在三棱锥中,为等边三角形,平面且,则二面角的平面角的正切值为()A、B、C、D、10、若函数在是增函数,则的取值范围是()A、B、C、D、11、如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.B.6C.D.412、已知分别为双曲线的左、右焦点,为双曲线右支上任意一点,若的最小值为,则双曲线离心率的取值范围为()A、B、C、D、二、填空题(本大题共4小题,每小题5分,满分20分).13、的展开式中的系数为.214、若命题“”为真命题,则的取值范围为.15、过点作直线与圆交于M、N两点,若=8,则的方程为___________.16、如图,把椭圆的长轴分成等份,过每个分点作轴的垂线交椭圆的上半部分于七个点,是椭圆的一个焦点,则.三、解答题(本大题共6小题,满分70分)17、已知:,:,若是的充分不必要条件。求实数的取值范围。18、某同学在篮球场上进行投篮训练,先投“2分的篮”2次,每次投中的概率为,每投中一次得2分,不中得0分;再投“3分的篮”1次,每次投中的概率为,投中得3分,不中得0分,该同学每次投篮的结果相互独立,假设该同学要完成以上三次投篮。(1)求该同学恰好有2次投中的概率;(2)求该同学所得分X的分布列。19、如图,直三棱柱中,是等边三角形,是的中点.3(1)求证://平面;(2)若,求与平面所成角的正弦值.20、某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.(1)求进入决赛的人数;(2)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在9.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.21、已知抛物线的焦点为,为上异于原点的任意一点,过点的直线交于另一点,交轴的正半轴于点,且有.当点的横坐标为时,为正三角形.(1)求的方程;(2)若直线,且和有且只有一个公共点,证明直线过定点,并求出定点坐标;422、设函数(为常数,是自然对数的底数).(1)当时,求函数的单调区间;(2)若函数在内存在两个极值点,求的取值范围.宜昌2017年3月月考答案一、选择题1—5DBADA6—10BCCAD11—12BC二、填空题13、3514、15、或16、35三、解答题(18)(本题满分12分)证明:(I)因为三棱柱111ABCABC是直三棱柱,所以四边形11AACC是矩形。连结1AC交1AC于O,则O是1AC的中点,又D是BC的中点,所以在1ADC中,1//ODAB。因为1AB平面1ADC,OD平面1ADC,所以1//AB平面1ADC。(II)因为ABC是等边三角形,D是BC的中点,所以ADBC。以D为原点,建立如图所示空间坐标系Dxyz。由已知12ABBB,得:(0,0,0)D,(3,0,0)A,1(3,0,2)A,1(0,1,2)C.则(3,0,0)DA�,1(0,1,2)DC�,设平面1ADC的法向量为(,,)nxyz。5由100nDAnDC����,得到3020xyz,令1z,则0x,2y,所以(0,2,1)n.又1(3,0,2)DA�,得10320122nDA��。所以1...