一平行射影1.(2016·陕西咸阳高二检测)直角三角形在平面上的正射影不可能是()A.一个点B.线段C.直角三角形D.钝角三角形解析当直角三角形与投影面垂直时,正射影是线段;当直角三角形斜边与投影面平行,三角形与投影面不平行时,正射影是钝角三角形;当直角三角形与投影面平行时,正射影是直角三角形.但直角三角形在平面上的正射影不可能是一个点.答案A2.两条异面直线m和n在平面α上的平行射影是()A.一条直线和直线外一个点B.两条相交直线C.两条平行直线D.以上都有可能解析当m和n中有一条直线与投影方向平行时,它们的平行射影是一个点和一条直线;否则是两条平行直线或相交直线.答案D3.若一个三角形的平行投影仍是一个三角形,则下列结论正确的是()A.内心的平行投影还是内心B.重心的平行投影还是重心C.垂心的平行投影还是垂心D.外心的平行投影还是外心解析如果三角形的平行投影仍是三角形,但三角形的形状通常将发生变化,此时三角形的各顶点、各边的位置也会发生变化,而重心、垂心、外心这些由顶点和边确定的点通常随着发生变化,而内心则始终是原先角平分线的交点,所以仍是新三角形的内心.答案A4.导学号19110050已知Rt△ABC的斜边BC在平面α内,则△ABC的两条直角边在平面α内的射影与斜边组成的图形只能是()A.一条线段B.一个锐角三角形C.一个钝角三角形1D.一条线段或一个钝角三角形解析(1)当顶点A在平面α内的正射影A'在BC所在直线上时,两条直角边在平面α内的正射影是一条线段,与斜边组成的图形是线段,如图①.(2)当顶点A在平面α内的正射影A'不在BC所在直线上时,如图②.∵AA'⊥α,∴AA'⊥A'B,AA'⊥A'C.∴A'B
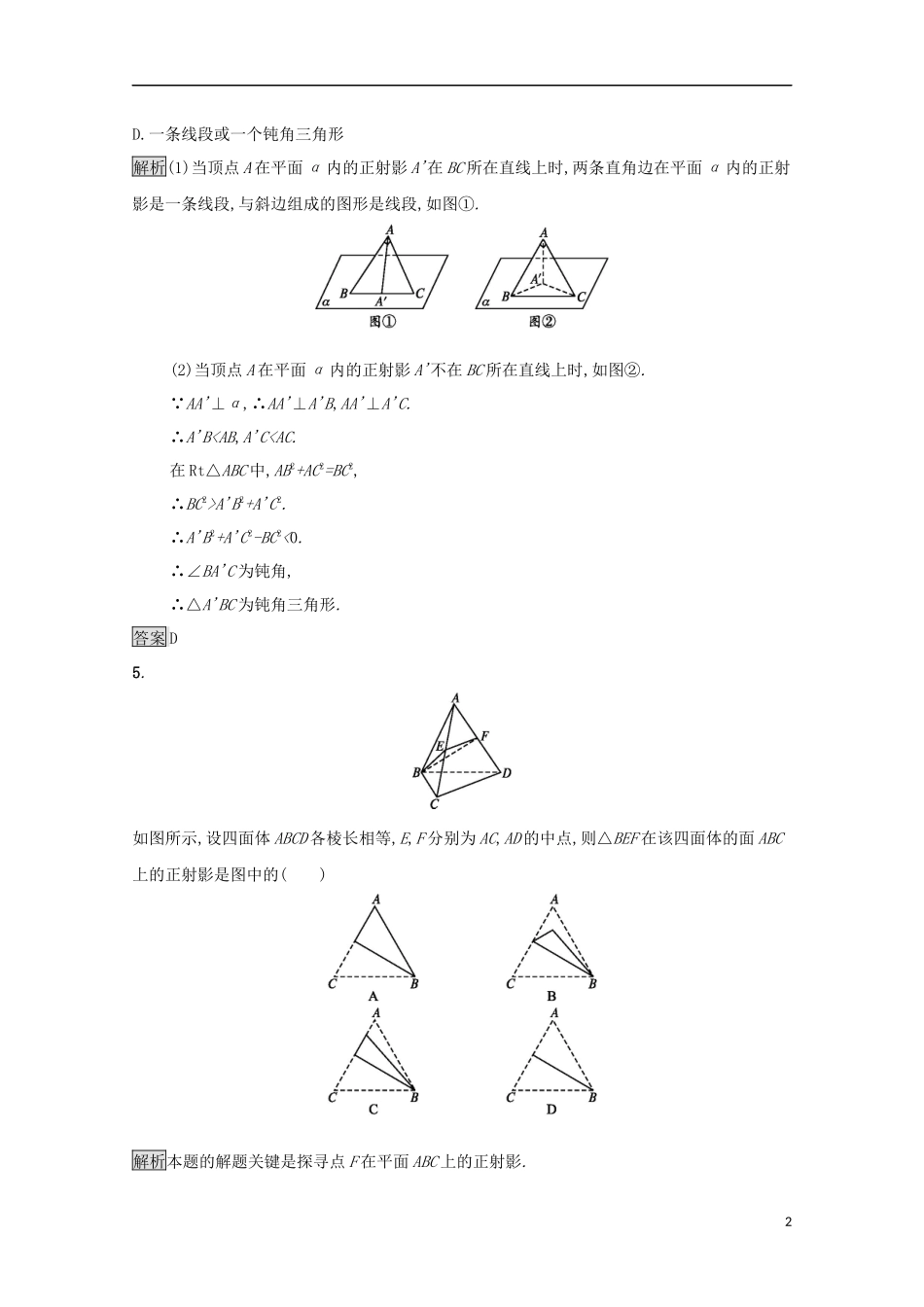
A'B2+A'C2.∴A'B2+A'C2-BC2<0.∴∠BA'C为钝角,∴△A'BC为钝角三角形.答案D5.如图所示,设四面体ABCD各棱长相等,E,F分别为AC,AD的中点,则△BEF在该四面体的面ABC上的正射影是图中的()解析本题的解题关键是探寻点F在平面ABC上的正射影.2因为BE=BF,所以△BEF为等腰三角形,故点F在平面ABC上的正射影不在AC上而在△ABC内部,又因为EF与CD平行,而CD与平面ABC不垂直,所以F点在平面ABC上的正射影不在直线BE上,从而B成立.故选B.答案B6.两条相交直线的平行射影是.解析两条相交直线的平行射影,仍然有一公共点,因为两条相交直线的交点的平行射影必在两条直线的平行射影上,从而有两条相交直线的平行射影为两条相交直线,或者是一条直线.答案两条相交直线或一条直线7.用平面α截圆柱OO',当OO'与平面α所成的角等于时,截面是一个圆.答案90°8.(2016·山西太原高二检测)若P为△ABC所在平面外一点,PA,PB,PC与平面ABC所成角均相等,又PA与BC垂直,则△ABC的形状可能是(将你认为正确的序号全填上).①正三角形;②等腰三角形;③非等腰三角形;④等腰直角三角形.解析设点P在底面ABC上的射影为O,由PA,PB,PC与平面ABC所成角均相等,得OA=OB=OC,即点O为△ABC的外心,又由PA⊥BC,得OA⊥BC,又OB=OC,得直线AO垂直平分BC,∴AB=AC,即△ABC必为等腰三角形,故应填①②④.答案①②④9.已知点P是△ABC所在平面α外一点,点O是点P在平面α内的正射影.(1)若点P到△ABC的三个顶点等距离,则点O是△ABC的什么心?(2)若点P到△ABC的三边距离相等,且点O在△ABC的内部,则点O是△ABC的什么心?(3)若PA,PB,PC两两相互垂直,则点O是△ABC的什么心?解如图所示.(1)若PA=PB=PC,O点为点P在平面ABC上的正射影,故有OA=OB=OC,故点O为△ABC的外心.(2)由点P到△ABC的三边距离相等,则点O到△ABC的三边距离相等,故点O为△ABC的内心.3(3)PO⊥平面ABC,PA⊥BC,因此OA⊥BC,同理可证:OB⊥AC,OC⊥AB,故点O为△ABC的垂心.10.导学号19110051如图,△ABC是边长为2的正三角形,BC∥平面α,A,B,C在平面α的同侧,它们在α内的正射影分别为A',B',C',若△A'B'C'为直角三角形,BC与α间的距离为5,求A到α的距离.解∵BC∥平面α,且△ABC是正三角形,∴A'B'=A'C',B'C'=BC=2.又∵△A'B'C'为直角三角形,∴∠B'A'C'=90°.∴2A'C'2=B'C'2=BC2=4.∴A'C'2=2.设A到α的距离AA'=x,过点C作CD⊥AA',垂足为D.由题意知CD∥C'A',CD=A'C',AD=AA'-CC'=x-5.在Rt△ACD中,AD2+CD2=AC2,∴(x-5)2+2=22.∴x=5±√2.故A到α的距离为5±√2.45