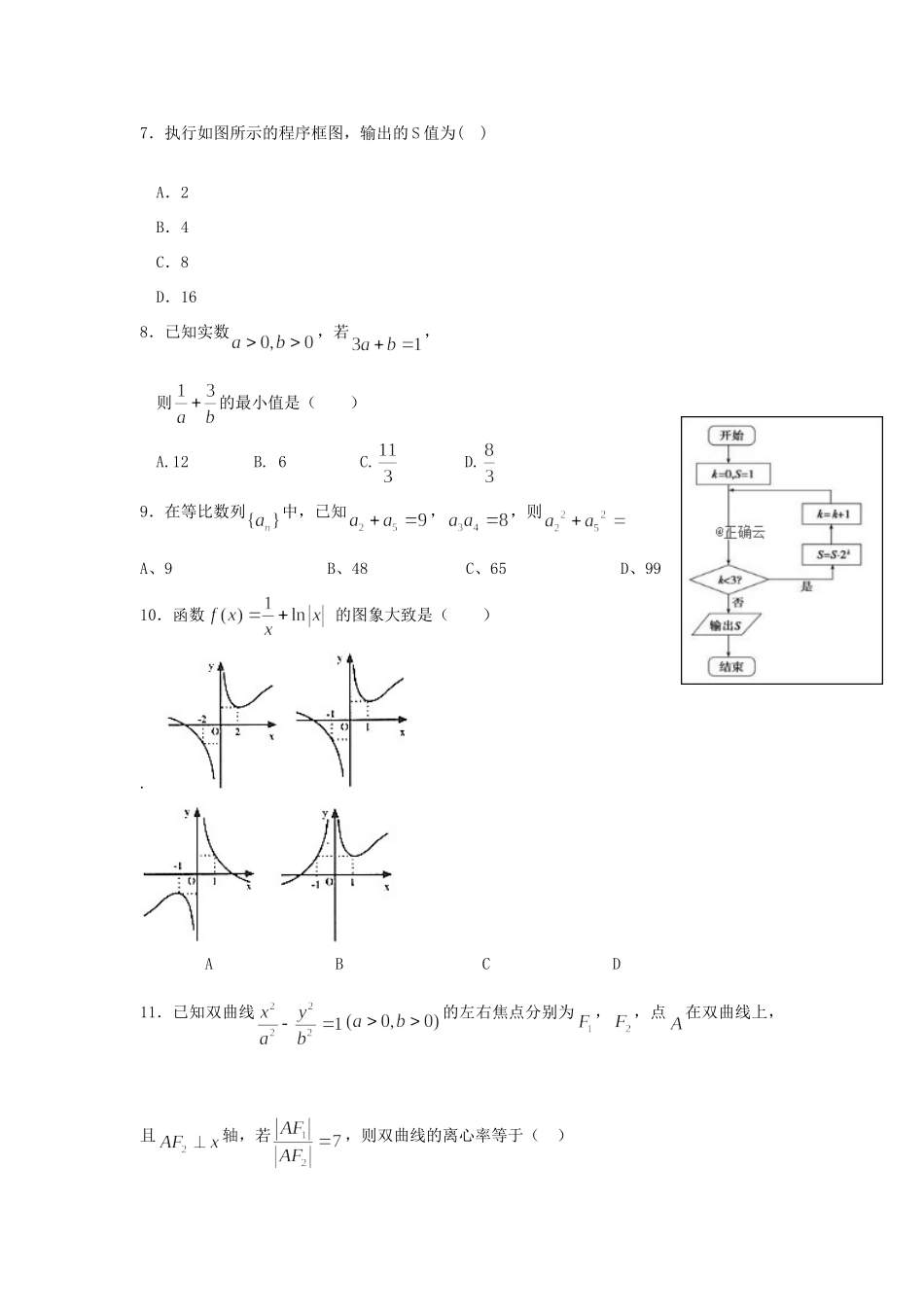
内蒙古师范大学锦山实验学校2019-2020学年高二数学上学期期中试题文第I卷(选择题共60分)一、选择题:(本题共12小题,每题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)1.设集合则=()A.[0,2)B.[0,2]C.(2,3]D.[2,3]2.若复数满足,则复数()A.B.C.D.3.设则p是q的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件4.已知向量=(2,2),2+=(4,2),则向量,的夹角的余弦值为()A.B.-C.D.-5.为了得到函数的图象,只需把函数的图象()A.向左平行移动个单位长度B.向左平行移动个单位长度C.向右平行移动个单位长度D.向右平行移动个单位长度6.已知一个空间几何体的三视图如右图,其中正视图,侧视图都是由半圆和矩形组成,根据图中标出的尺寸,可得这个几何体的表面积是A、B、C、D、7.执行如图所示的程序框图,输出的S值为()A.2B.4C.8D.168.已知实数,若,则的最小值是()A.12B.6C.D.9.在等比数列中,已知,,则A、9B、48C、65D、9910.函数的图象大致是().ABCD11.已知双曲线的左右焦点分别为,,点在双曲线上,且轴,若,则双曲线的离心率等于()A.B.C.D.712.是定义在上的奇函数,且,当时,,则当时,不等式的解集是()A.B.C.D.第II卷(非选择题共90分)二、填空题:(本题共4小题,每题5分,共20分。)13.某高级中学共有900名学生,现用分层抽样的方法从该校学生中抽取1个容量为90的样本,其中高一年级抽40人,高三年级抽20人.则该校高二年级学生人数为_________.14.已知变量满足约束条件则的最大值为.15.设曲线在x=1处的切线方程是,则________;16.已知直线与圆相交,弦长为2,则____________.三、解答题:(本题共6小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤。)17.(本题10分)己知函数(1)求函数的最小正周期。(2)记△ABC的内角A、B、C的对边长分别为a、b、c,若,,b=1,c=,求a的值.18.(本题12分)已知公差不为0的等差数列{}na中,且1413,,aaa成等比数列.(1)求数列{}na的通项公式;(2)试推导数列1{}nS的前n项和nT的表达式。19.(本题12分)某大学高等数学老师这学期分别用两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:(Ⅰ)依茎叶图判断哪个班的平均分高?(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的列联表,并判断“能否甲班乙班合计优秀不优秀合计在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”下面临界值表仅供参考:0.150.100.050.0250.0100.0050.0012.0722.7063.8415.0246.6357.87910.828(参考公式:其中)20.(本题12分)如图,在三棱柱中,底面,,为线段的中点.(1)求证:直线平面;(2)求三棱锥的体积.21.(本题12分)已知椭圆C:(a>b>0)上的点M与两个焦点构成的三角形周长为,椭圆C的离心率为(1)求椭圆C的标准方程.(2)已知点Q(),动直线过右焦点,且直线l与椭圆C交于A,B两点,证明:为定值.22.(本题12分)已知函数.(1)求函数的的单调区间;(2)若恒成立,试确定实数的取值范围。参考答案1.A【解析】 M={x|(x+4)(x-2)<0}=(-4,2)N={x|0≤x≤3}=[0,3],∴M∩N=[0,2)故选A2.C【解析】试题分析:.选C.3.B【解析】p真:;q真:,显然p是q的充分不必要条件.4.D【解析】由已知条件求得=(0,-2),所以cos〈,〉==.5.B【解析】由函数,所以只需把函数的图象沿着x轴向左平移个单位而得到,故选B.6.D【解析】该几何体下方是一个圆柱,上面是半球组合成的,圆柱的高是1,半径是1,球的半径是1,表面积为7.C【解析】试题分析:程序执行中的数据变化如下:不成立,输出8.A【解析】实数,则,当且仅当时取等号.故本题正确答案是A9.C【解析】试题分析:由得,故。选C。10.B【解析】特值法:特殊点11.A【解析】略12.D【解析】试题分析:当时,不等...