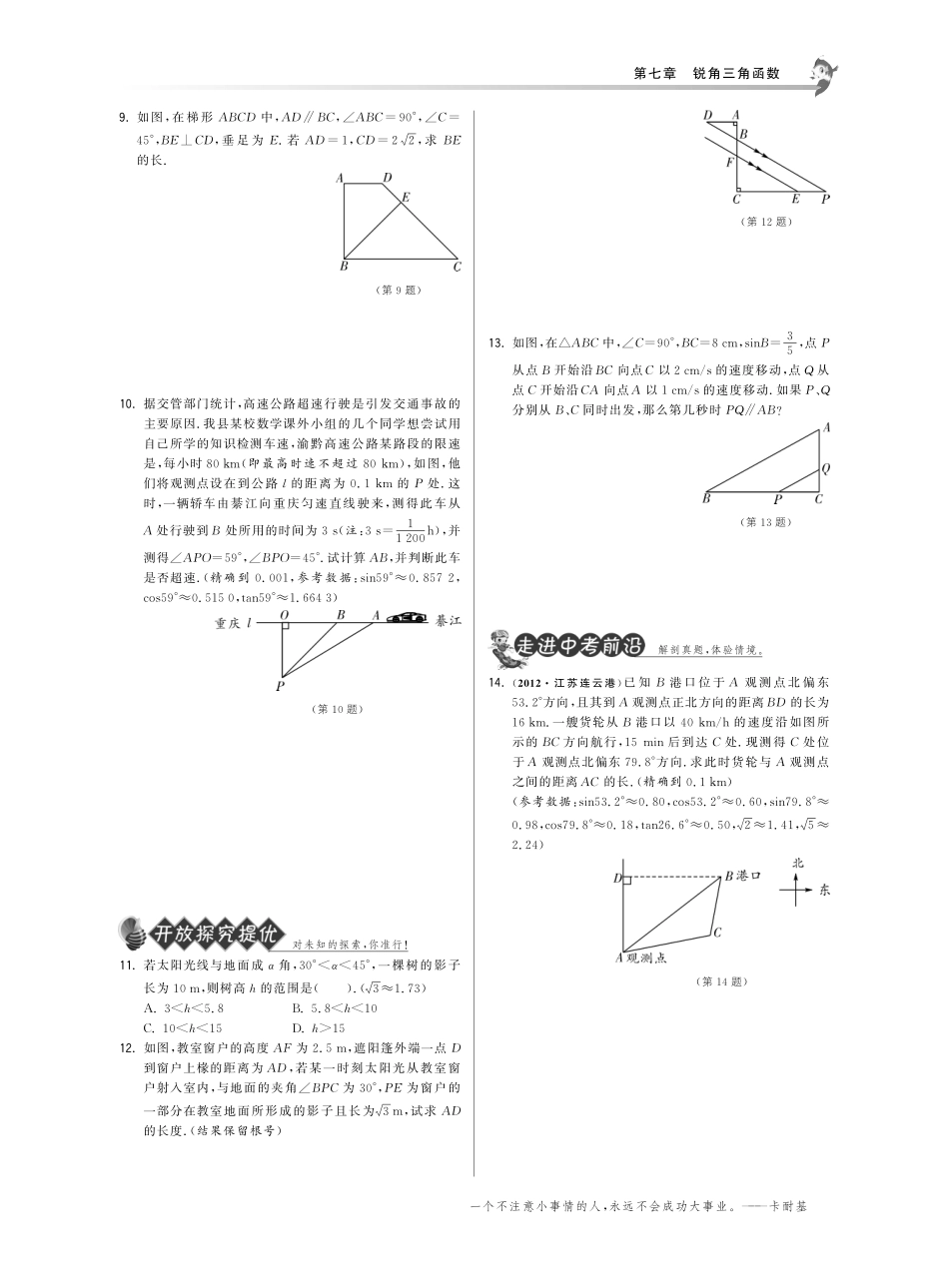
知识是一种快乐,而好奇则是知识的萌芽.———培根7.6锐角三角函数的简单应用第1课时锐角三角函数的简单应用(1)1.会把现实生活中较简单的实际问题转化为直角三角形的问题.2.在解决实际问题的过程中进一步体会三角函数的意义.夯实基础,才能有所突破1.如图,从点C测得树的顶角为33°,BC=20m,则树高AB=m.(用计算器计算,结果精确到0.1m)(第1题)(第2题)2.如图,某地夏季中午,当太阳移到屋顶上方偏东时,光线与地面成α角,房屋朝南的窗子高AB=hm,如果要在窗子外面上方安装一个水平挡光板AC,使午间光线不能直接射入室内,那么挡光板AC的宽度为.3.如图,为测量一河两岸相对的两电线杆A、B间的距离,在距点A15m处的点C(AC⊥BA)测得∠ACB=50°,则A、B间的距离应为().(第3题)A.15sin50°mB.15cos50°mC.15tan50°mD.15tan50°m4.如图,秋千拉绳OB的长为3m,静止时,踏板到地面的距离BE长为0.6m(踏板的厚度忽略不计),当秋千拉绳由OB运动到OA时,拉绳OA与铅垂线OE的夹角为55°,请你计算此时该秋千踏板离地面的高度AD.(精确到0.1m,参考数据:tan55°≈1.4281,sin55°≈0.8192,cos55°≈0.5736)(第4题)5.某校九年级数学兴趣小组的同学开展了测量湘江宽度的活动.如图,他们在河东岸边的点A测得河西岸边的标志物B在它的正西方向,然后从点A处出发沿河岸向正北方向行进550m到点C处,测得B在点C的南偏西60°方向上,他们测得的湘江宽度是多少米?(结果保留整数,参考数据:2≈1.414,3≈1.732)(第5题)课内与课外的桥梁是这样架设的.6.若某人沿坡角为β的斜坡前进100m,则他上升的最大高度为().A.100sinβmB.100sinβmC.100cosβmD.100cosβm7.如图,AB是☉O的直径,CD是弦,且CD⊥AB,若BC=6,AC=8,则sin∠ABD的值是().A.43B.34C.35D.45(第7题)(第8题)8.如图,已知某河堤的横断面是梯形ABCD,BC∥AD,若迎水坡AB长13m,且tan∠BAE=125,则河堤的高BE为m.第七章锐角三角函数一个不注意小事情的人,永远不会成功大事业.———卡耐基9.如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠C=45°,BE⊥CD,垂足为E.若AD=1,CD=22,求BE的长.(第9题)10.据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是,每小时80km(即最高时速不超过80km),如图,他们将观测点设在到公路l的距离为0.1km的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3s(注:3s=11200h),并测得∠APO=59°,∠BPO=45°.试计算AB,并判断此车是否超速.(精确到0.001,参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)(第10题)对未知的探索,你准行!11.若太阳光线与地面成α角,30°<α<45°,一棵树的影子长为10m,则树高h的范围是().(3≈1.73)A.3<h<5.8B.5.8<h<10C.10<h<15D.h>1512.如图,教室窗户的高度AF为2.5m,遮阳篷外端一点D到窗户上椽的距离为AD,若某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,PE为窗户的一部分在教室地面所形成的影子且长为3m,试求AD的长度.(结果保留根号)(第12题)13.如图,在△ABC中,∠C=90°,BC=8cm,sinB=35,点P从点B开始沿BC向点C以2cm/s的速度移动,点Q从点C开始沿CA向点A以1cm/s的速度移动.如果P、Q分别从B、C同时出发,那么第几秒时PQ∥AB?(第13题)解剖真题,体验情境.14.(2012江苏连云港)已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km.一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后到达C处.现测得C处位于A观测点北偏东79.8°方向.求此时货轮与A观测点之间的距离AC的长.(精确到0.1km)(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°...