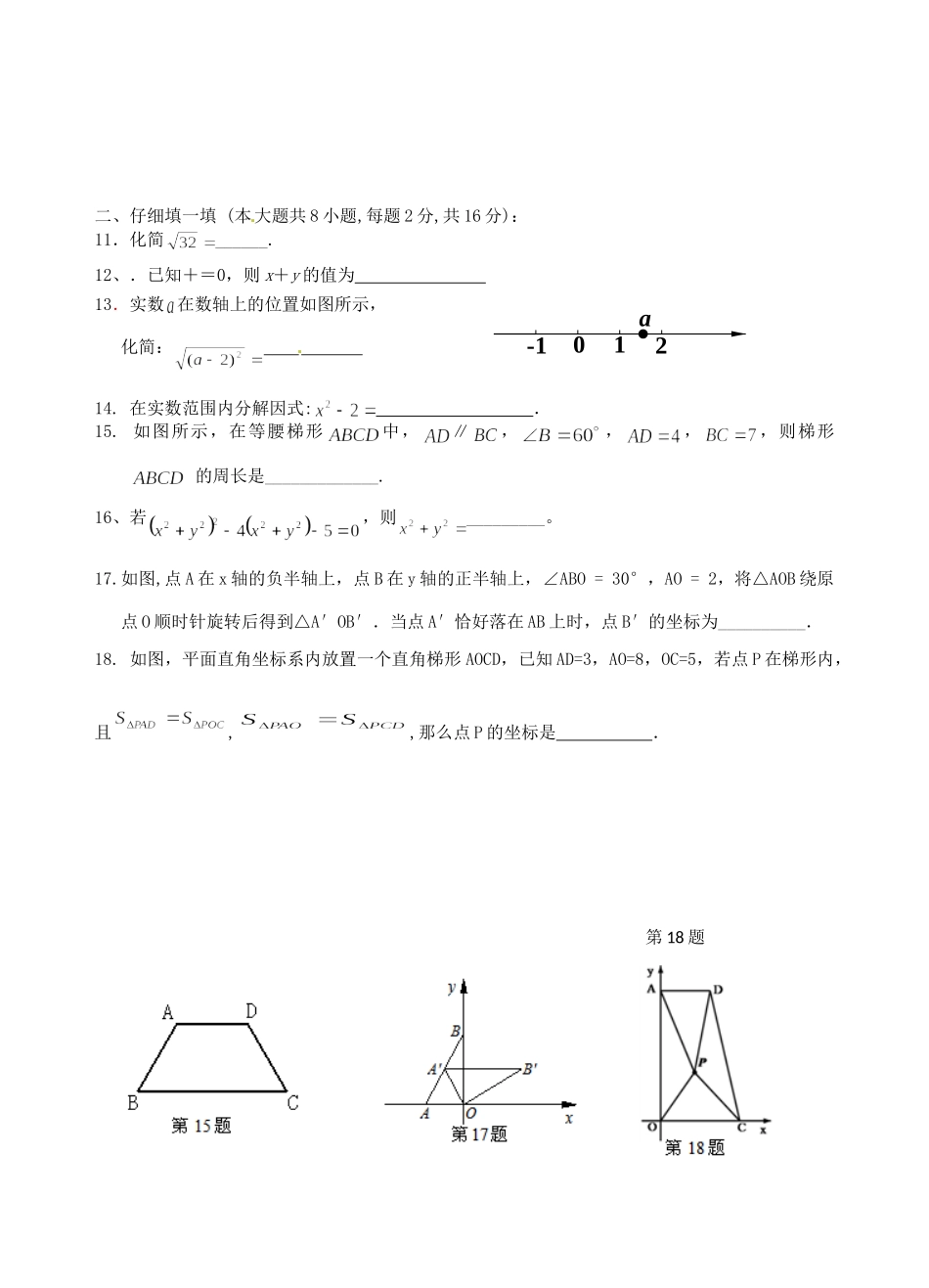
江苏省宜兴外国语学校2013届九年级数学第一次阶段性测试(9月)试题(无答案)一.精心选一选(每小题3分,共30分,每题的四个选项中,只有一个符合题意):1.二次根式1a中,字母a的取值范围是()A、B、a≤1C、a≥1D、2.的结果是()A.B.C.D.23.已知是一个整数,则满足条件的正整数的最小值为()A.1B.2C.3D.46.在菱形ABCD中,两条对角线AC=2,BD=4,则此菱形的周长为()A.B.2C.5D.45.用配方法解一元二次方程时可配方得()A.B.C.D.6、若方程是关于的一元二次方程,则的值为()A.B、C、D、以上都不对7、方程x(x-1)=2的两根为()A.x1=0,x2=1B.x1=0,x2=-1C.x1=1,x2=-2D.x1=-1,x2=28、在下列二次根式中,是最简二次根式的式子有()个。A、2B、3C、1D、09、对任意实数x,多项式的值是一个()A.正数B.负数C.非负数D.无法确定10.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2010个正方形的面积为()A.B.C.DOABCDA1B1C1A2C2B2xy2009235201049520084954018235二、仔细填一填(本大题共8小题,每题2分,共16分):11.化简______.12、.已知+=0,则x+y的值为13.实数在数轴上的位置如图所示,化简:14.在实数范围内分解因式:.15.如图所示,在等腰梯形中,∥,,,,则梯形的周长是_____________.16、若,则_________。17.如图,点A在x轴的负半轴上,点B在y轴的正半轴上,∠ABO=30°,AO=2,将△AOB绕原点O顺时针旋转后得到△A′OB′.当点A′恰好落在AB上时,点B′的坐标为__________.18.如图,平面直角坐标系内放置一个直角梯形AOCD,已知AD=3,AO=8,OC=5,若点P在梯形内,且,,那么点P的坐标是.-1012a第18题第18题三、认真解一解:(本大题共10大题,共84分,请在答题指定区域内作答,解答应写出必要的计算过程、推演步骤或文字说明):19、(3×4分)计算:(1)(2)(3)20、(3×4分)解方程:(1)(2)(3)21、(6分)已知x1=-1是方程x2+mx-5=0的一个根,求m的值及方程的另一个根x2.22、(6分)先化简,再求值:,其中a=1+.23.(8分)已知:如图,□ABCD中,∠ABC的平分线交AD于E,∠CDA的平分线交BC于F.(1)求证:△ABE≌△CDF;(2)连接EF、BD,求证:EF与BD互相平分.24.(10分)阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如,善于思考的小明进行了以下探索:设(其中a、b、m、n均为正整数),则有∴这样小明就找到了一种把部分的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:(1)当均为正整数时,若用含m、n的式子分别表,得:a=,b=;(2)利用所探索的结论,任意找一组正整数a、b、m、n填空:+=(+);(3)若,且a、m、n均为正整数,求的值.ABCDEF(第23题)25.(8分)在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:.(2)若△DEF三边的长分别为、、,请在图1的正方形网格中画出相应的△DEF,并利用构图法求出它的面积:.(3)利用第2小题解题方法完成下题:如图2,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17,且△PQR、△BCR、△DEQ、△AFP的面积相等,则六边形花坛ABCDEF的面积为.26、(10分)如图,在直角梯形ABCD中,AB∥CD,∠C=90°,AB=6cm,CD=10cm,AD=5cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向点B移动,点Q以1cm/s的速度向点D移动,当一个动点到达终点时另一个动点也随之停止运动.(1)经过几秒钟,点P、Q之间的距离为5cm?(2)连结PD,是否存在某一时刻,使得PD恰好平分∠APQ?若存在,求出此时的移动时间;若不存在...