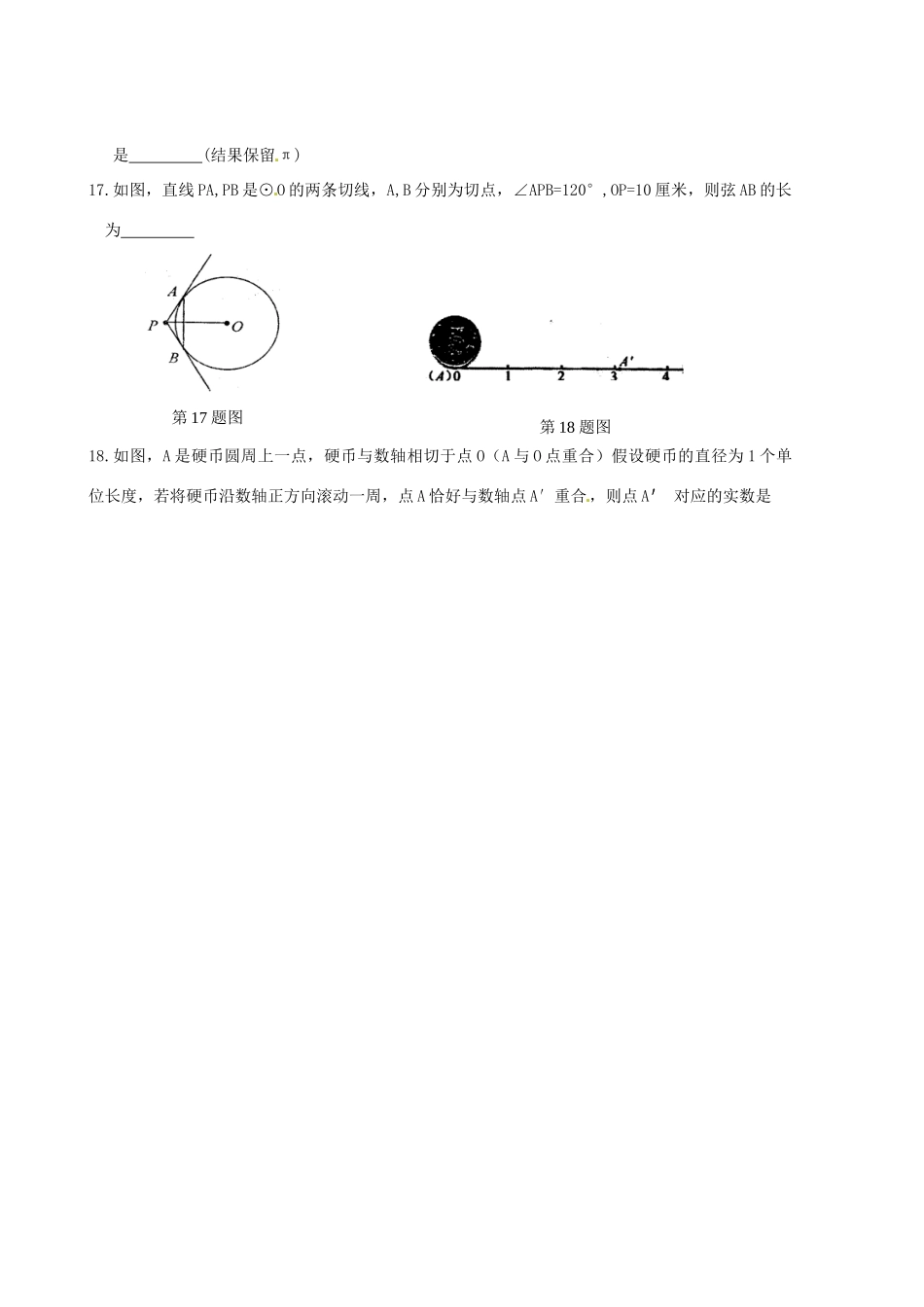
九年级第一学期第二次阶段考试试卷数学试题(满分150分)一、选择题(每小题3分,共30分)1.二次根式2、、、、、中,最简二次根式的个数是()A.2个B.3个C.4个D.5个2.在方程x+=2,(3-x)(2+x)=4,x2+x=y,2x-x2=x3中一元二次方程()A.0个B.1个C.2个D.3个3.下列命题中,真命题是()A.两条对角线相等的四边形是矩形B.两条对角线垂直的四边形是菱形C.两条对角线垂直且相等的四边形是正方形D.两条对角线相等的平行四边形是矩形4.某型号的手机连续两次降价,每个售价由原来的1185元降到了580元,设平均每次降价的百分率为x,则列出方程正确的是()A.580(1+x)2=1185B.1185(1+x)2=580C.580(1-x)2=1185D.1185(1-x)2=5805.下列计算正确的是()A.—=B.=-=1C.(2-)(2+)=1D.=36.如图,已知AC是⊙O的直径,AB=CD=DE∠AOB=40°,那么∠AOE=()A.40°B.100°C.60°D.1207.下列说法中,错误的有()①一组数据的标准差是它的差的平方;②数据8,9,10,11,11的众数是2;----第6题图③如果数据x1,x2,…,xn的平均数为x,那么(x1-x)+(x2-x)+…(xn-x)=0;④数据0,-1,1,-2,1的中位数是1.A.4个B.3个C.2个D.1个8.关于x的一元二次方程kx2+2x—1=0有两个不相等的实数根,则k的取值范围是()A.k>-1B.k>1C.k≠0D.k>-1且k≠09.如图,在Rt△ABC中,AC=5,BC=12,⊙O分别为AB、AC相切,切点分别为E、C,则⊙O的半径是()A.B.C.D.10.如图,直角坐标系中,⊙O的半径为1,则直线y=-x+与⊙O的位置关系是()A.相离B.相交C.相切D.以上三种情形都有可能二、填空题(每小题3分,共24分)11.在函数y=中自变量x的取值范围是12.顺次连结矩形的各边中点,所得的四边形是13.一元二次方程(a-1)x2+x+a2-1=0有一根为0,a的值为14.圆和圆有多种位置关系,与图中不同的圆和圆的位置关系是15.如图,PA、PB、DE分别切⊙O于A、B、C,如果△PDE的周长为8,那么PA=16.如果圆锥的底面周长为20π,侧面展开后所得扇形的圆心角是l20°,则该圆锥的侧面积第9题图第10题图第14题图第15题图是(结果保留π)17.如图,直线PA,PB是⊙O的两条切线,A,B分别为切点,∠APB=120°,OP=10厘米,则弦AB的长为18.如图,A是硬币圆周上一点,硬币与数轴相切于点O(A与O点重合)假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴点A′重合,则点A′对应的实数是第17题图第18题图三、解答题(96分)19.计算(每题5分,共10分)(1)×÷(-)(2)(+2)(3-5)20.解下列方程(每题6分,共12分)(1)8y2-2=4y(配方法)(2)2(2x-3)2-3(2x-3)=021已知:平行四边形ABCD中,对角线AC和BD相交于点O,M,N,分别是OA,OC的中点,求证:BM=DN,BM∥DN.(8分)22.已知:如图,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线与AB的延长线交于点D。若∠CAB=30°,AB=30,求BD的长。(8分)23.如图,AB是⊙O的弦,OC⊥OA交AB于点C,过B的直线交OC的延长线于点E,当CE=BE时,直线BE与⊙O有怎样的位置关系?请说明理由。(10分)24.(10分)如图①、②、③中,点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.(1)求图①中,∠APD的度数;(4分)(2)图②中,∠APD的度数为,图③中,∠APD的度数为;(2分)(3)根据前面探索,你能否将本题推广到一般的正n边形情况.若能,以正六边形为例画出示意图,直接写出结论:若不能,请说明理由.(4分)25.(10分)某市绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格l0元/千克在该市收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存ll0天,同时,平均每天有6千克的香菇损坏不能出售.(1)若存放x天后,将这批香菇一次性出售,设这批香菇的销售总金额为y元,试写出y与x之间的函数关系式.(4分)(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额—收购成本—各种费用)(6分)26.(12分)如图,在单位长度为1的...