6.1余弦函数的图像VIP免费

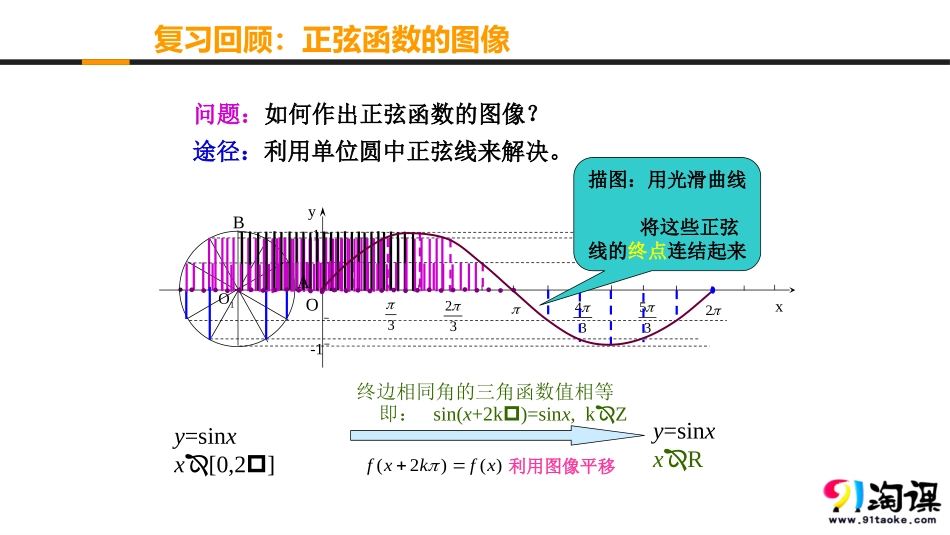
§6余弦函数的图像与性质合阳县第二高级中学：宋崇辉1.会用“图像变换法”和“五点法”作余弦函数的图像.（重点）2.掌握余弦函数y=cosx的图像和性质.（重点）3.会应用余弦函数y=cosx的图像与性质解决一些简单问题.（难点）复习回顾：正弦函数的图像问题：如何作出正弦函数的图像？途径：利用单位圆中正弦线来解决。y=sinxx[0,2]O1Oyx33234352-11y=sinxxR终边相同角的三角函数值相等即：sin(x+2k)=sinx,kZ)()2(xfkxf描图：用光滑曲线将这些正弦线的终点连结起来利用图像平移AB正弦、余弦函数的图像x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322三角函数三角函数线余弦函数探究1：如何作出余弦函数的图像？yxO-1PMcos=OM注意：三角函数线是有向线段！余弦线OM问题1：能否利用单位圆中余弦线来解决？答案：能。问题2：能否利用正弦函数的图像平移得到余弦函数的图像？提示：x2sinxcos答案：能。探究1：如何作出余弦函数的图像？x6yo--12345-2-3-41余弦函数的图像正弦函数的图像x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同探究1：如何作出余弦函数的图像？最高点：最低点：与x轴的交点：(0,1)，3(,0)2(2,1)(,1)(,0)2，在函数的图像上，起关键作用的点有：cos,[0,2]yxx五点法作图-1-oxy--1-3232656734233561126探究2：余弦函数的性质有哪些？问题2：能否类比正弦函数的性质得到余弦函数的性质？类比正弦性质得出余弦函数性质x6yo--12345-2-3-41y=sinx(xR)x6o--12345-2-3-41yy=cosx(xR)定义域值域周期性xRy[-1,1]T=2xyo-23-2-11函数在那些区间上是单调递增的？在那些区间是单调递减的？余弦函数的单调性y=cosx(xR)xcosx22-……0……-1010-1增区间为其值从-1增至1[+2k,2k],kZ减区间为，其值从1减至-1[2k,2k+],kZyxo--1234-2-31223252722325类比正弦性质得出余弦函数性质sin(-x)=-sinx(xR)y=sinx(xR)x6yo--12345-2-3-41是奇函数x6o--12345-2-3-41ycos(-x)=cosx(xR)y=cosx(xR)是偶函数定义域关于原点对称正弦、余弦函数的奇偶性类比正弦性质得出余弦函数性质p2最小正周期为偶函数)(cos)cos()(xfxxxf==-=-12min-=+=ykx时，当pp12max==ykx时，当p[]上是减函数；在pppp22,2++Îkkx[]上是增函数；在pppkkx2,2-Î[]1,1-R、定义域：1、值域：2、单调性：3、最值：4、奇偶性：5、周期性：6结论：余弦函数y=cosx的性质例1画出函数的简图，根据图像讨论函数的性质．cos1yx=-xy=cosx00-1-2-10０－１０１解：列表1y=cosx-1y=cosx-1yxo--1234-2-31223252722325-2y=cosx函数y=cosx-1定义域值域奇偶性周期性单调性最值R[-2,0]偶函数2πx2k,2k(kZ)x2k,2k(kZ)当时，函数是增加的；当时，函数是减少的x2k(kZ)0x(2k1)(kZ)2当时，最大值为；当时，最小值为通过本节学习应掌握以下几点:1.余弦函数y=cosx的图像和性质及其运用.2.用“五点法”和“图像变换法”作余弦函数的图像.三角函数三角函数线余弦函数思考：如何利用单位圆中余弦线作出余弦函数的图像？yxO-1PMcos=OM注意：三角函数线是有向线段！余弦线OM，xycos2,0x