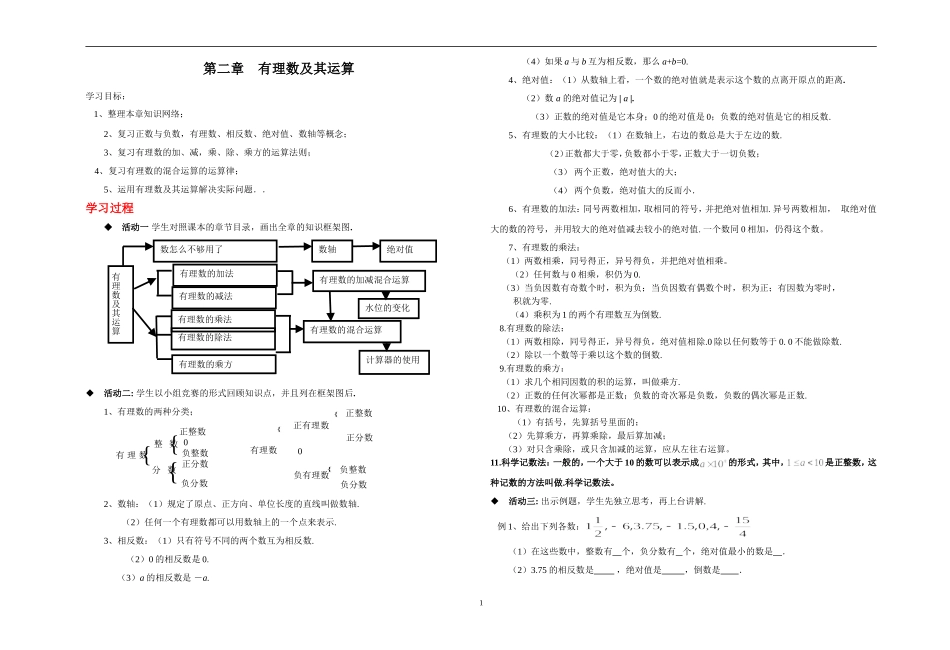
1第二章有理数及其运算学习目标:1、整理本章知识网络;2、复习正数与负数,有理数、相反数、绝对值、数轴等概念;3、复习有理数的加、减,乘、除、乘方的运算法则;4、复习有理数的混合运算的运算律;5、运用有理数及其运算解决实际问题..学习过程活动一学生对照课本的章节目录,画出全章的知识框架图.活动二:学生以小组竞赛的形式回顾知识点,并且列在框架图后.1、有理数的两种分类;2、数轴:(1)规定了原点、正方向、单位长度的直线叫做数轴.(2)任何一个有理数都可以用数轴上的一个点来表示.3、相反数:(1)只有符号不同的两个数互为相反数.(2)0的相反数是0.(3)a的相反数是-a.(4)如果a与b互为相反数,那么a+b=0.4、绝对值:(1)从数轴上看,一个数的绝对值就是表示这个数的点离开原点的距离.(2)数a的绝对值记为|a|.(3)正数的绝对值是它本身;0的绝对值是0;负数的绝对值是它的相反数.5、有理数的大小比较:(1)在数轴上,右边的数总是大于左边的数.(2)正数都大于零,负数都小于零,正数大于一切负数;(3)两个正数,绝对值大的大;(4)两个负数,绝对值大的反而小.6、有理数的加法:同号两数相加,取相同的符号,并把绝对值相加.异号两数相加,取绝对值大的数的符号,并用较大的绝对值减去较小的绝对值.一个数同0相加,仍得这个数。7、有理数的乘法:(1)两数相乘,同号得正,异号得负,并把绝对值相乘。(2)任何数与0相乘,积仍为0.(3)当负因数有奇数个时,积为负;当负因数有偶数个时,积为正;有因数为零时,积就为零.(4)乘积为1的两个有理数互为倒数.8.有理数的除法:(1)两数相除,同号得正,异号得负,绝对值相除.0除以任何数等于0.0不能做除数.(2)除以一个数等于乘以这个数的倒数.9.有理数的乘方:(1)求几个相同因数的积的运算,叫做乘方.(2)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.10、有理数的混合运算:(1)有括号,先算括号里面的;(2)先算乘方,再算乘除,最后算加减;(3)对只含乘除,或只含加减的运算,应从左往右运算。11.科学记数法:一般的,一个大于10的数可以表示成的形式,其中,是正整数,这种记数的方法叫做.科学记数法。活动三:出示例题,学生先独立思考,再上台讲解.例1、给出下列各数:(1)在这些数中,整数有个,负分数有个,绝对值最小的数是.(2)3.75的相反数是,绝对值是,倒数是.数怎么不够用了数轴绝对值有理数的加减混合运算有理数的加法水位的变化有理数及其运算有理数的减法有理数的乘法有理数的除法有理数的乘方有理数的混合运算计算器的使用{{{有理数整数分数正整数负整数正分数0负分数有理数正有理数负有理数正分数0正整数负整数负分数2(3)这些数用数轴上的点表示后,与原点距离最远的数是_____.(4)这些数从小到大,用“<”号连接起来:.例2、(1)写出在数轴上和原点距离等于4.3个单位的点所表示的数;(2)写出在数轴上和表示-5的点距离等于4个单位的点所表示的数;(3)若将第2题中所得到的左边的点向右移动1.5个单位,右边的点向左移动2.5个单位,则各表示什么数?例3、已知|x|=3,|y|=2,且x