北京市宣武区2) 试题VIP专享VIP免费

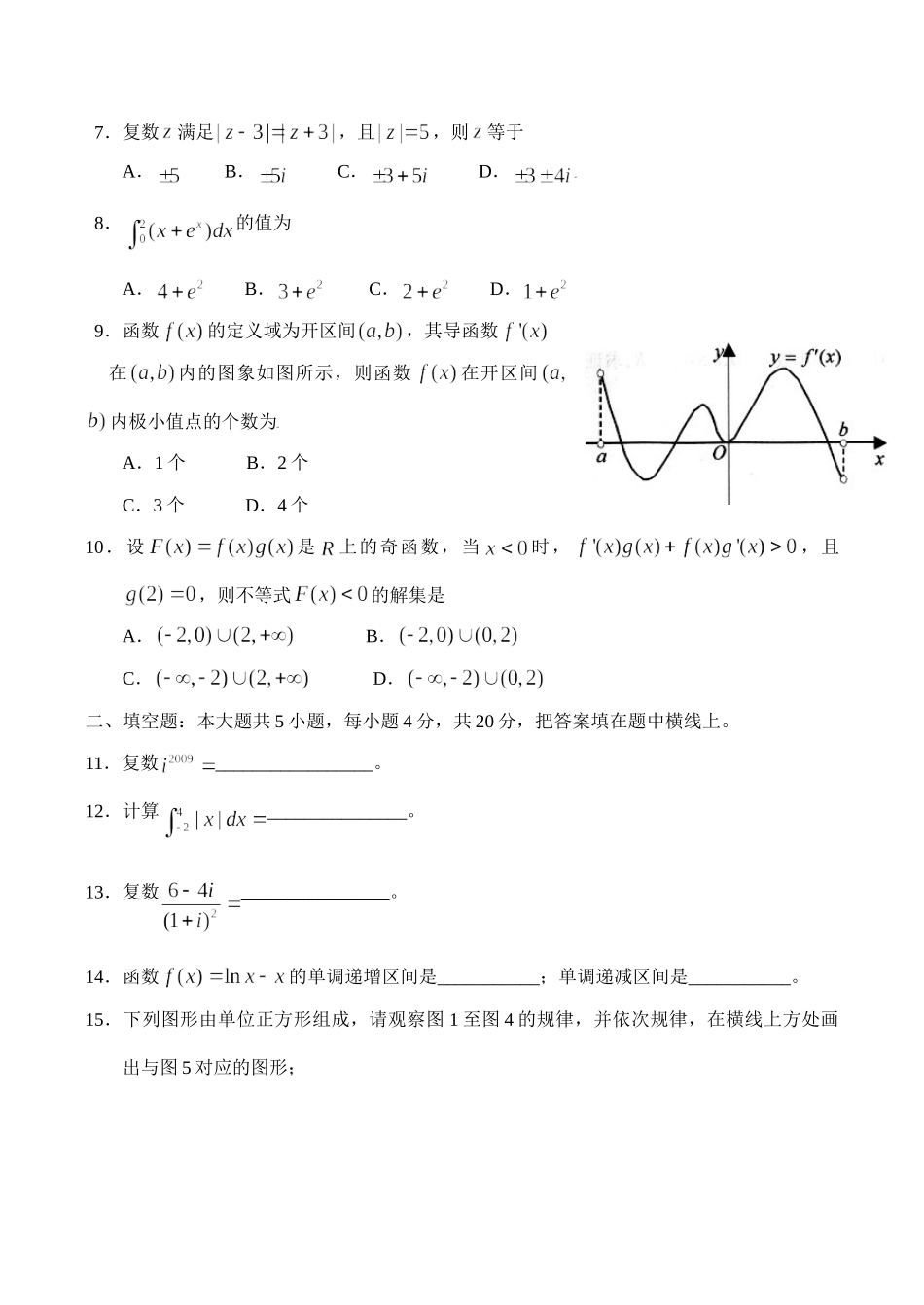
北京市宣武区08-09学年高二下学期模块数学（选修2—2）一、选择题：本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合要求的。1．已知函数在处的导数为1，则等于A．2B．C．1D．2．函数的导数为A．B．C．D．3．曲线上某点切线的斜率等于4，则此点坐标为A．和B．C．和D．4．若复数，则“是纯虚数”是“”的A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5．函数的图象如图所示，若，则等于A．B．C．0D．6．若实数，则与的大小关系是A．B．C．D．不确定7．复数满足，且，则等于A．B．C．D．8．的值为A．B．C．D．9．函数的定义域为开区间，其导函数在内的图象如图所示，则函数在开区间内极小值点的个数为A．1个B．2个C．3个D．4个10．设是上的奇函数，当时，，且，则不等式的解集是A．B．C．D．二、填空题：本大题共5小题，每小题4分，共20分，把答案填在题中横线上。11．复数_________________。12．计算_______________。13．复数________________。14．函数的单调递增区间是___________；单调递减区间是___________。15．下列图形由单位正方形组成，请观察图1至图4的规律，并依次规律，在横线上方处画出与图5对应的图形；按图示的规律画下去，则第个图的正方形个数可以是___________（。三、解答题：本大题共4个小题，每小题10分，共40分，解答应写出文字说明，证明过程或演算步骤。16．已知实数求证：。17．已知函数（I）若是的极值点，求在上的最大值；（Ⅱ）若函数是上的单调递增函数，求实数的取值范围。18．已知函数、，曲线经过点，且在点处的切线垂直于轴，设。（I）用分别表示和；（Ⅱ）当取得最小值时，求函数的单调递增区间。19．已知数列的前项和为。（I）求的值；（Ⅱ）猜想的表达式；并用数学归纳法加以证明。北京市宣武区2008—2009学年度第二学期高中新课程模块检测高中数学（选修2—2）参考答案及评分标准一、选择题：本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合要求的题号12345678910答案CABBCABDAD二、填空题：本大题共5小题，每小题4分，共20分，把答案填在题中横线上。11．i12．1013．14．增区间为（0，1）；减区间是，15．三、解答题：本大题共4小题，每小题10分，共40分，解答应写出文字说明，证明过程或演算步骤。16．证明：由，可知；由，可知；同向不等式相加即可得证。17．解：（I）。，即，解得或（舍去）当变化时，、的变化情况如下表：13（3，5）5015因此，当时，在区间[1，5]上有最大值是（Ⅱ）是上的单调递增函数转化为在上恒成立。从而有的，解得。18．解：（I）经过点；由切线垂直于轴可知，从而有，（Ⅱ）因为而，当且仅当，即时取得等号。因为时为单调递增函数，即为单调递增区间19．解：（I）（Ⅱ）猜想数学归纳法证明：（1）当时，猜想成立；（2）假设时猜想成立，即有：，则时，因为，即：；由假设可知；从而有时，猜想成立；由（1）（2）可知，成立www.jk.zy.w.com