九年级数学上册 第二章 圆 22 圆的对称性专题讲义(pdf，无答案)(新版)苏科版试卷VIP免费

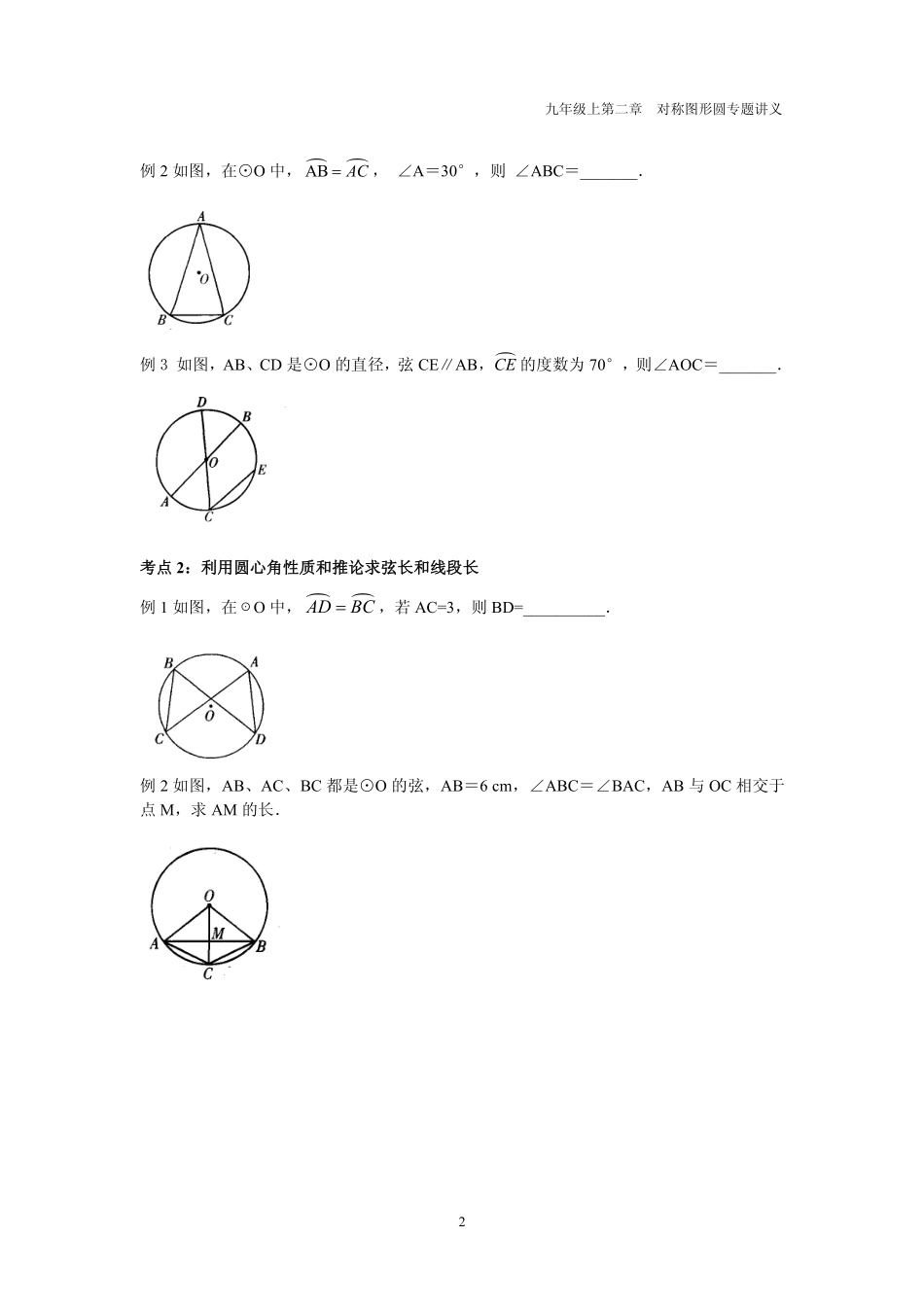
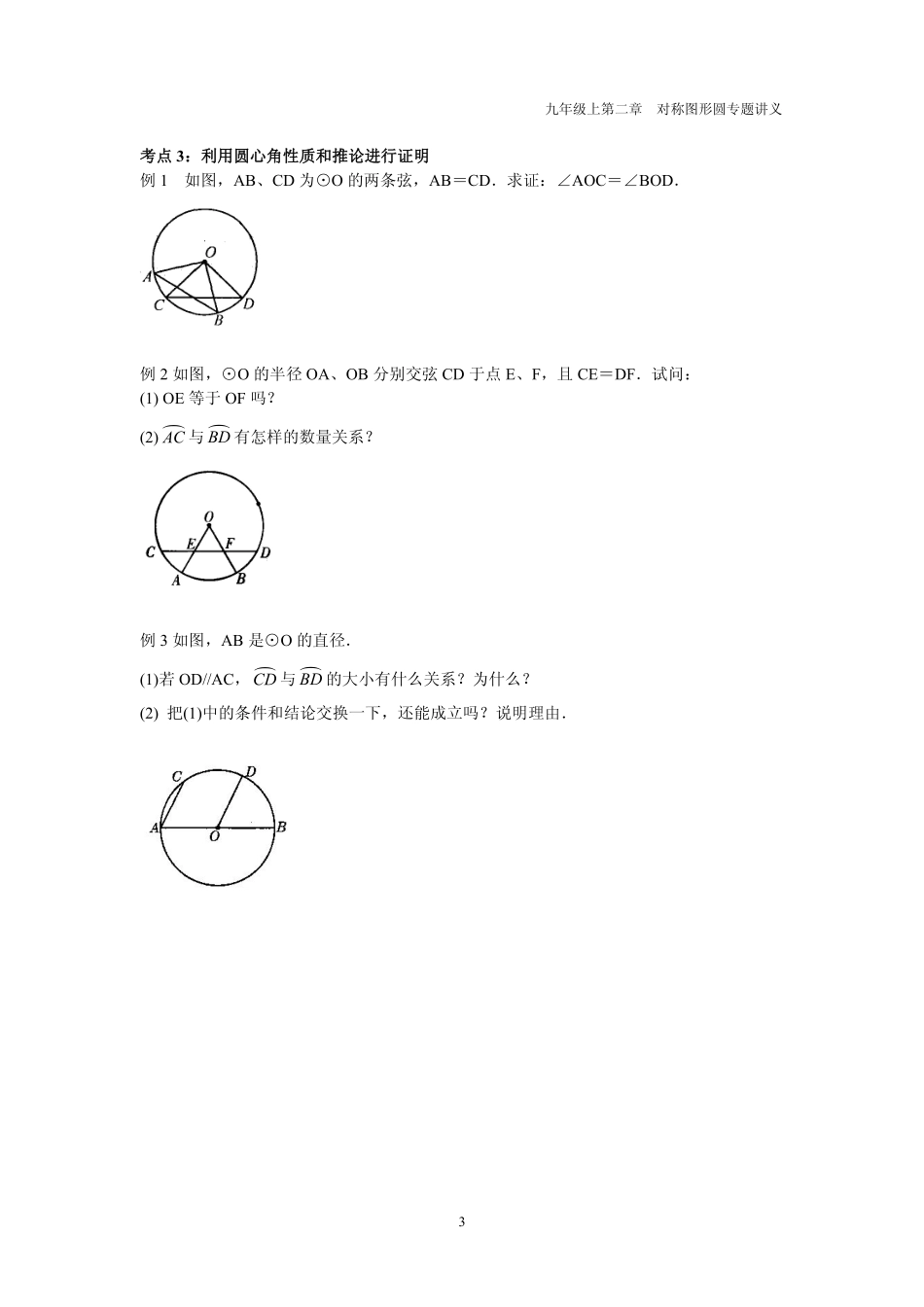
九年级上第二章对称图形圆专题讲义1对称图形——圆专题讲义2.2圆的对称性课标知识与能力目标1.理解圆的对称性及有关性质2.掌握圆心角、弧、弦之间的关系3.掌握垂径定理，并会运用定理解决有关问题知识点1：圆的对称性圆是中心对称图形，对称中心是圆心；圆也是轴对称图形，对称轴是经过圆心的任意一条直线。注意：（1）圆的对称轴有无数条。（2）圆还具有旋转不变性，即圆绕圆心旋转任何角度后，仍与自身重合。典型例题考点：命题判定例1下列说法正确的是（）A.直径是圆的对称轴B.经过圆心的直线是圆的对称轴C.与圆相交的直线是圆的对称轴D.与半径垂直的直线是圆的对称轴知识点2：圆心角、弧、弦之间的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么他们所对应的其余各组量都分别相等。典型例题考点1：利用圆心角性质和推论求角度例1如图，在⊙O中，ACBD，∠1＝25°，则∠2＝_______．九年级上第二章对称图形圆专题讲义2例2如图，在⊙O中，ABAC，∠A＝30°，则∠ABC＝_______．例3如图，AB、CD是⊙O的直径，弦CE∥AB，CE的度数为70°，则∠AOC＝_______．考点2：利用圆心角性质和推论求弦长和线段长例1如图，在☉O中，ADBC，若AC=3，则BD=__________．例2如图，AB、AC、BC都是⊙O的弦，AB＝6cm，∠ABC＝∠BAC，AB与OC相交于点M，求AM的长．九年级上第二章对称图形圆专题讲义3考点3：利用圆心角性质和推论进行证明例1如图，AB、CD为⊙O的两条弦，AB＝CD．求证：∠AOC＝∠BOD．例2如图，⊙O的半径OA、OB分别交弦CD于点E、F，且CE＝DF．试问：(1)OE等于OF吗？(2)AC与BD有怎样的数量关系？例3如图，AB是⊙O的直径．(1)若OD//AC，CD与BD的大小有什么关系？为什么？(2)把(1)中的条件和结论交换一下，还能成立吗？说明理由．九年级上第二章对称图形圆专题讲义4知识点3：圆心角的度数与它所对的弧的度数的关系1.1的弧：将顶点在圆心的周角等分成360份时，每一份的圆心角是1的角。因为同圆中相等的圆心角所对的弧相等，所以整个圆也被等分成360份，我们把1的圆心角所对的弧叫做1的弧。2.圆心角的度数与它所对的弧的度数的关系：圆心角的度数与它所对的弧的度数相等。注意：（1）圆心角的度数与它所对的弧的度数相等，不是指角与弧相等（角与弧是两个不同的图形）（2）度数相等的角为等角，但度数相等的弧不一定是等弧。典型例题考点：求圆心角例1如图，AB、CD是⊙O的直径，弦CE∥AB，CE的度数为40°，则∠AOC＝_______°．例2☉O的一条弦AB把圆分成2：3两部分，则弦所对的圆心角为__________0．九年级上第二章对称图形圆专题讲义5能力提优题型1：圆心角性质和推论例1如图，在☉O中，弦AD∥BC，DA=DC，∠AOC=1600，则∠BCO的度数为()A．200B．600C.400D．500例2如图，小华从一个圆形场地的A点出发，沿着与半径OA夹角为a的方向行走，走到场地边缘B点后，再沿着与半径OB夹角为a的方向折向行走．按照这种方式，小华第五次走到场地边缘时处于AB上，此时∠AOE=560，则a=__________0．例3如图，在△ABC中，∠A=700，☉O截△ABC的三边所得的弦长相等，则∠BOC的度数为__________0．题型2：利用圆心角性质和推论比较弦长和弧长的大小例1如图，在同圆中，若∠AOB＝2∠COD，则AB与2CD的大小关系是()A．AB>2CDB．AB<2CDC．AB＝2CDD．不能确定例2如图，在同圆中，若AB＝2CD，则AB与2CD的大小关系是()A．AB>2CDB．AB<2CDC．AB＝2CDD．不能确定九年级上第二章对称图形圆专题讲义6题型3：圆心角性质和推论与综合证明例1如图，AB，CD是⊙O的两条直径，过点A作AE//CD交⊙O于点E，连接BD，DE．求证：BD＝DE.例2如图，点O在∠MPN的平分线上，☉O分别交PN、PM于点A、B和点C、D．求证：∠PCO=∠NAO．九年级上第二章对称图形圆专题讲义7知识点4：垂径定理及垂径定理的推论1.垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。定理的条件：（1）直径，弦（2）直径垂直弦定理的结论：（1）弦被直径平分（2）弦所对的两条弧被平分2.垂径定理的推...