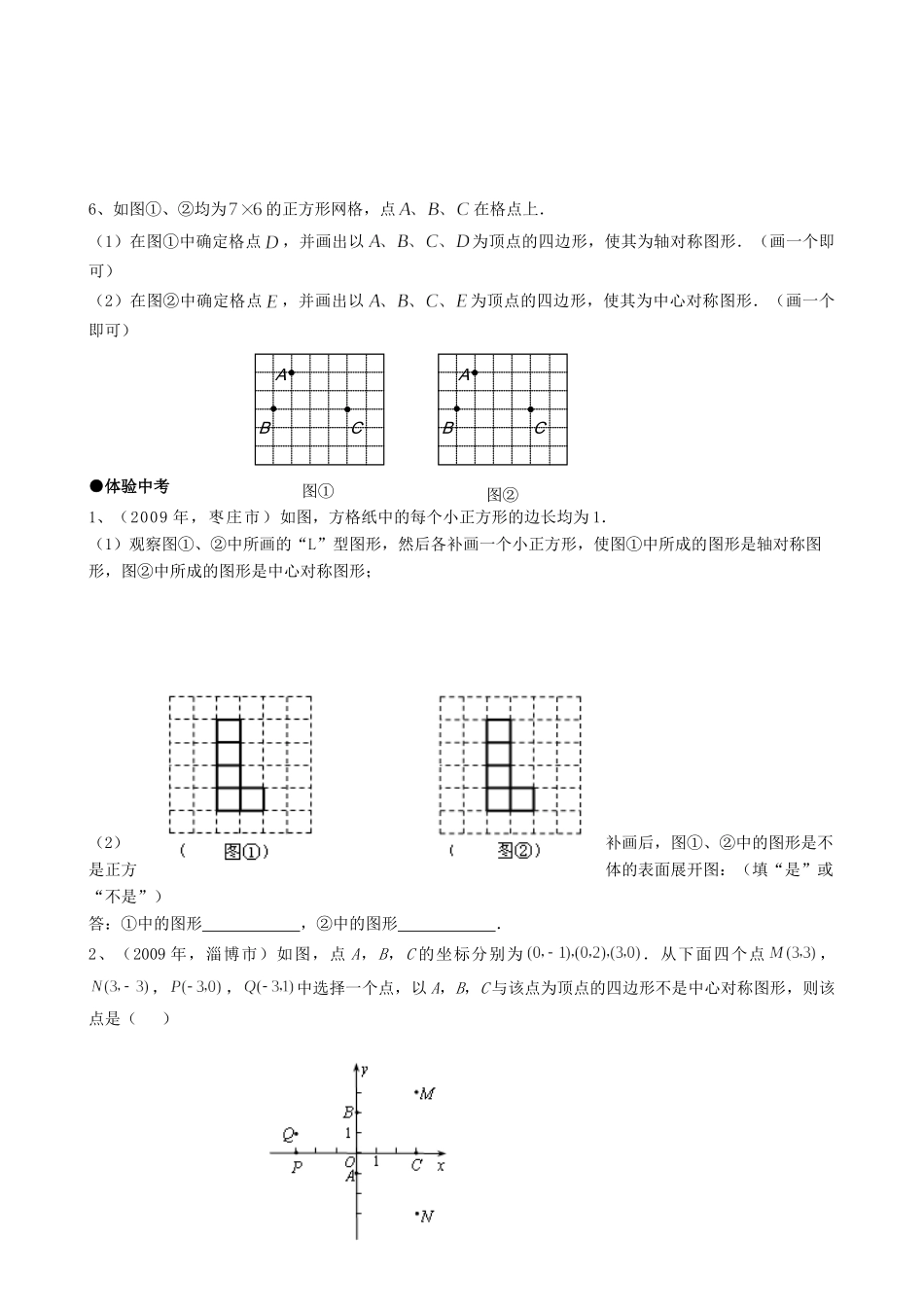
23.2中心对称(第三课时)◆随堂检测1、下列标志既是轴对称图形又是中心对称图形的是()ABCD2、已知点P(-b,2)与点Q(3,2)关于原点对称,则+b的值是________.3、已知,则点P()关于原点的对称点P′在()A.第一象限B.第二象限C.第三象限D.第四象限4、如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.提示:点P(x,y)关于原点的对称点为P′(-x,-y).◆典例分析已知△ABC,A(-3,2),B(-2,-1),C(2,3)利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的△A1B1C1.分析:要作出△ABC关于原点的对称图形,只要作出点A、点B和点C关于原点的对称点A′、B′、C′即可.依据中心对称的点的坐标特点:点P(x,y)关于原点的对称点P′的坐标为(-x,-y),可得A′、B′、C′三点的坐标.解:∵点P(x,y)关于原点的对称点为P′(-x,-y),∴△ABC的三个端点A(-3,2),B(-2,-1),C(2,3)关于原点的对称点分别为A′(3,-2)、B′(2,1)、C′(-2,-3).依次连结A′B′、B′C′、C′A′,便可得到所求作的△A′B′C′.xy(-3,2)(2,3)(-2,-1)CBA-2-1321-3O-112-23第12题_y_x_(-3,2)_(2,3)_(-2,-1)_C_B_A_-2_-1_3_2_1_-3_O_-1_1_2_-2_3-3-33OBA-2-21-1yx3-44221-1◆课下作业●拓展提高1、下列图形中,是轴对称图形但不是中心对称图形的2、已知点的坐标为,为坐标原点,连结,将线段绕点按逆时针方向旋转90°得,则点的坐标为()A、B、C、D、3、如图,四边形EFGH是由四边形经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形旋转得到四边形EFGH时的旋转中心用有序数对表示是____________.4、直线上有一点P(3,),则点P关于原点的对称点P′为________.5、如图所示,请在网格中作出△ABC关于点O对称的△A1B1C1,再作出△A1B1C1绕点B1逆时针旋转90°后的△A2B1C2.6、如图①、②均为的正方形网格,点在格点上.(1)在图①中确定格点,并画出以为顶点的四边形,使其为轴对称图形.(画一个即可)(2)在图②中确定格点,并画出以为顶点的四边形,使其为中心对称图形.(画一个即可)●体验中考1、(2009年,枣庄市)如图,方格纸中的每个小正方形的边长均为1.(1)观察图①、②中所画的“L”型图形,然后各补画一个小正方形,使图①中所成的图形是轴对称图形,图②中所成的图形是中心对称图形;(2)补画后,图①、②中的图形是不是正方体的表面展开图:(填“是”或“不是”)答:①中的图形,②中的图形.2、(2009年,淄博市)如图,点A,B,C的坐标分别为.从下面四个点,,,中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是()ABC图①ABC图②A.MB.NC.PD.Q参考答案:◆随堂检测1、A.2、2.∵点P(-b,2)与点Q(3,2)关于原点对称,∴,∴.3、D.∵当时,点P()在第二象限,∴则点P关于原点的对称点P′在第四象限.故选D.4、解:线段AB的两个端点A(0,-1),B(3,0)关于原点的对称点分别为A′(1,0),B′(-3,0),连结A′B′,就可得到与线段AB关于原点对称的线段A′B′.(图略)◆课下作业●拓展提高1、A.2、C.画图可得点的坐标为.3、(5,2).4、(-3,-6).将点P(3,)代入得,,∴对称点P′为(-3,-6).5、图略.6、解:(1)如图:(2)如图:●体验中考1、(1)如下图:(2)图①—1(不是)或图①—2(是),图②(是)2、C.