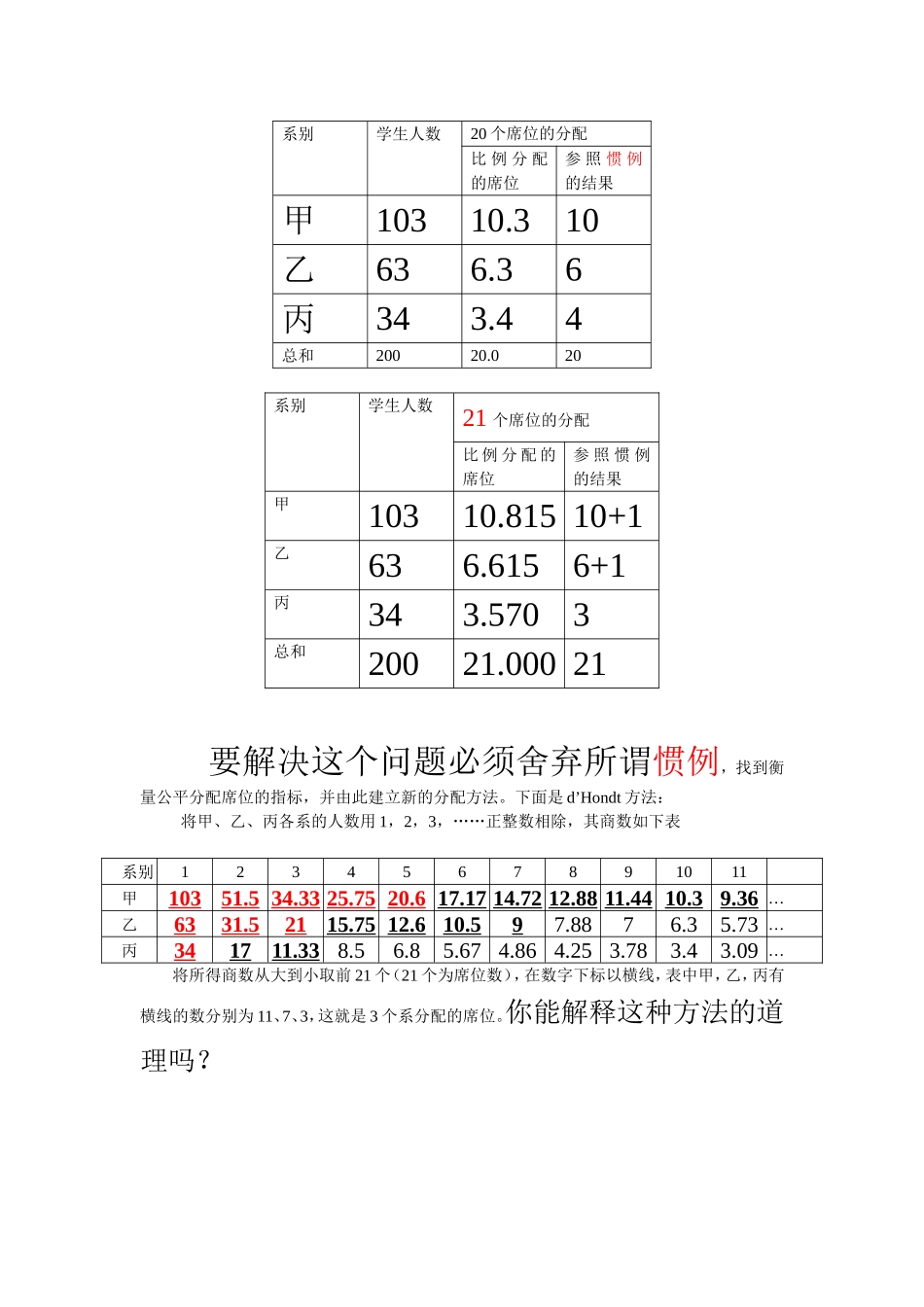
公平的席位问题(比例的应用)某学校有三个系共200个学生,其中甲系100名,乙系60名,丙系40名,若学生代表会建议设20个席位,公平而又简单的席位分配办法是按学生人数的比例分配,显然甲、乙、丙分别占有10、6、4个席位。现在丙系有6名学生转入甲乙两系,各系人数如下表第二列所示。仍按比例(表中第三列)分配席位时出现了小数(表中的第4列),在将取得整数的19席分配完毕后,三系同意剩下的1席参照所谓惯例分给比例中的小数最大的丙系,于是三系仍分别占有10,6,4席(表中第5列)。因为有20个席位的代表会议在表决提案时可能出现10:10的局面,会议决定增加1个代表席位。他们按照上述方法重新分配席位,计算结果见表第6、7两列。显然这个结果对丙系太不公平了,因为总席位增加了1席,而丙系却由4席减为3席。按照比例并参照惯例的席位分配系别学生人数20个席位的分配比例分配的席位参照惯例的结果甲10310.310乙636.36丙343.44总和20020.020系别学生人数21个席位的分配比例分配的席位参照惯例的结果甲10310.81510+1乙636.6156+1丙343.5703总和20021.00021要解决这个问题必须舍弃所谓惯例,找到衡量公平分配席位的指标,并由此建立新的分配方法。下面是d’Hondt方法:将甲、乙、丙各系的人数用1,2,3,……正整数相除,其商数如下表系别1234567891011甲10351.534.3325.7520.617.1714.7212.8811.4410.39.36…乙6331.52115.7512.610.597.8876.35.73…丙341711.338.56.85.674.864.253.783.43.09…将所得商数从大到小取前21个(21个为席位数),在数字下标以横线,表中甲,乙,丙有横线的数分别为11、7、3,这就是3个系分配的席位。你能解释这种方法的道理吗?