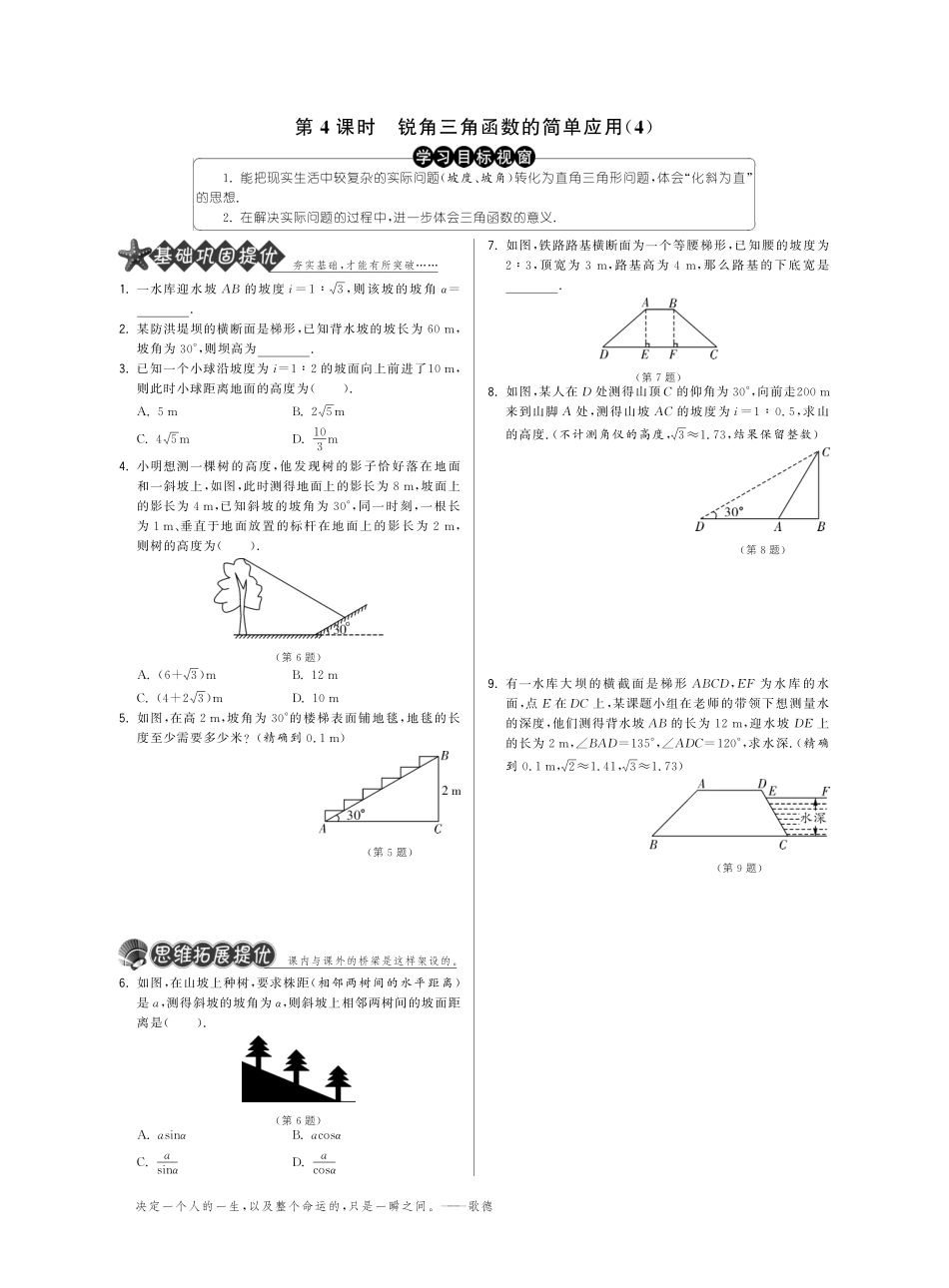
决定一个人的一生,以及整个命运的,只是一瞬之间.———歌德第4课时锐角三角函数的简单应用(4)1.能把现实生活中较复杂的实际问题(坡度、坡角)转化为直角三角形问题,体会“化斜为直”的思想.2.在解决实际问题的过程中,进一步体会三角函数的意义.夯实基础,才能有所突破1.一水库迎水坡AB的坡度i=1∶3,则该坡的坡角α=.2.某防洪堤坝的横断面是梯形,已知背水坡的坡长为60m,坡角为30°,则坝高为.3.已知一个小球沿坡度为i=1∶2的坡面向上前进了10m,则此时小球距离地面的高度为().A.5mB.25mC.45mD.103m4.小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8m,坡面上的影长为4m,已知斜坡的坡角为30°,同一时刻,一根长为1m、垂直于地面放置的标杆在地面上的影长为2m,则树的高度为().(第6题)A.(6+3)mB.12mC.(4+23)mD.10m5.如图,在高2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要多少米?(精确到0.1m)(第5题)课内与课外的桥梁是这样架设的.6.如图,在山坡上种树,要求株距(相邻两树间的水平距离)是a,测得斜坡的坡角为α,则斜坡上相邻两树间的坡面距离是().(第6题)A.asinαB.acosαC.asinαD.acosα7.如图,铁路路基横断面为一个等腰梯形,已知腰的坡度为2∶3,顶宽为3m,路基高为4m,那么路基的下底宽是.(第7题)8.如图,某人在D处测得山顶C的仰角为30°,向前走200m来到山脚A处,测得山坡AC的坡度为i=1∶0.5,求山的高度.(不计测角仪的高度,3≈1.73,结果保留整数)(第8题)9.有一水库大坝的横截面是梯形ABCD,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12m,迎水坡DE上的长为2m,∠BAD=135°,∠ADC=120°,求水深.(精确到0.1m,2≈1.41,3≈1.73)(第9题)第七章锐角三角函数言必信,行必果.———孔子10.庞亮和李强相约周六去登山,庞亮从北坡山脚C处出发,以24m/min的速度攀登,同时,李强从南坡山脚B处出发.如图,已知小山北坡的坡度(i=1∶3),山坡长为240m,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A?(将山路AB、AC看成线段,结果保留根号)(第10题)对未知的探索,你准行!11.如图,甲、乙两艘捕捞船同时从A港出海捕鱼,甲船以每小时152km的速度沿西偏北30°方向前进,乙船以每小时15km的速度沿东北方向前进.甲船航行2h后到达C处,此时甲船发现渔具丢在乙船上,于是,甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.问:(1)甲船从C处追赶上乙船用了多少时间?(2)甲船追赶乙船的速度为每小时多少千米?(第11题)12.台风是一种自然灾害,如图,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.据气象观测,在沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现正以15km/h的速度沿北偏东30°方向往C处移动,且台风中心风力不变.若城市所受风力达到或超过四级,则称为受台风影响.该城市是否会受到这次台风的影响?若会受台风影响,台风影响该城市的持续时间有多长?该城市受到台风影响的最大风力为几级?若不受台风的影响,请说明理由.(第12题)解剖真题,体验情境.13.(2012江苏泰州)如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.(1)求居民楼AB的高度;(2)求C、A之间的距离.(精确到0.1m,参考数据:2≈1.41,3≈1.73,6≈2.45)(第13题)第4课时锐角三角函数的简单应用(4)1.30°2.30m3.B4.A5.5.5m6.D7.15m8.162m9.6.7m10.过点A作AD⊥BC,垂足为D.(第10题)在Rt△ADC中,由i=1∶3,得tanC=13=33,∴∠C=30°.∴AD=12AC=12×240=120(m).在Rt△ABD中,∠B=45°,∴AB=2A...