九年级数学下册 281 锐角三角函数定义检测1 新人教版试卷VIP免费

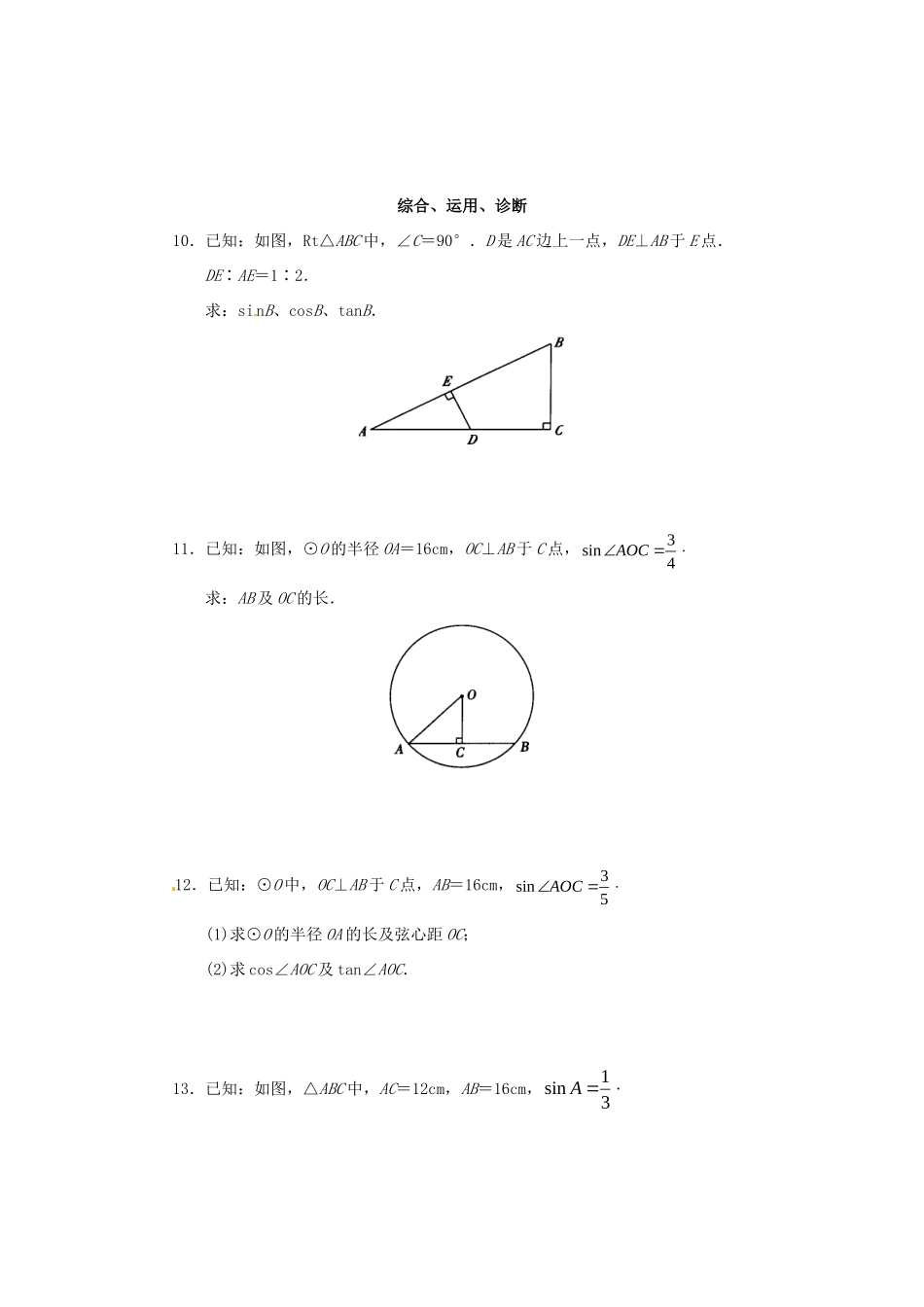
课题：锐角三角函数定义检测学习要求理解一个锐角的正弦、余弦、正切的定义．能依据锐角三角函数的定义，求给定锐角的三角函数值．课堂学习检测一、填空题1．如图所示，B、B′是∠MAN的AN边上的任意两点，BC⊥AM于C点，B′C′⊥AM于C′点，则△B'AC′∽______，从而ACBABCCB)()(，又可得①BACB______，即在Rt△ABC中(∠C＝90°)，当∠A确定时，它的______与______的比是一个______值；②BACA______，即在Rt△ABC中(∠C＝90°)，当∠A确定时，它的______与______的比也是一个______；③CACB______，即在Rt△ABC中(∠C＝90°)，当∠A确定时，它的______与______的比还是一个______．第1题图2．如图所示，在Rt△ABC中，∠C＝90°．第2题图①斜边)(sinA＝______，斜边)(sinB＝______；②斜边)(cosA＝______，斜边)(cosB＝______；③的邻边AA)(tan＝______，)(tan的对边BB＝______．3．因为对于锐角的每一个确定的值，sin、cos、tan分别都有____________与它______，所以sin、cos、tan都是____________．又称为的____________．4．在Rt△ABC中，∠C＝90°，若a＝9，b＝12，则c＝______，sinA＝______，cosA＝______，tanA＝______，sinB＝______，cosB＝______，tanB＝______．5．在Rt△ABC中，∠C＝90°，若a＝1，b＝3，则c＝______，sinA＝______，cosA＝______，tanA＝______，sinB＝______，cosB＝______，tanB＝______．6．在Rt△ABC中，∠B＝90°，若a＝16，c＝30，则b＝______，sinA＝______，cosA＝______，tanA＝______，sinC＝______，cosC＝______，tanC＝______．7．在Rt△ABC中，∠C＝90°，若∠A＝30°，则∠B＝______，sinA＝______，cosA＝______，tanA＝______，sinB＝______，cosB＝______，tanB＝______．二、解答题8．已知：如图，Rt△TNM中，∠TMN＝90°，MR⊥TN于R点，TN＝4，MN＝3．求：sin∠TMR、cos∠TMR、tan∠TMR．9．已知Rt△ABC中，,12,43tan,90BCAC求AC、AB和cosB．综合、运用、诊断10．已知：如图，Rt△ABC中，∠C＝90°．D是AC边上一点，DE⊥AB于E点．DE∶AE＝1∶2．求：sinB、cosB、tanB．11．已知：如图，⊙O的半径OA＝16cm，OC⊥AB于C点，43sinAOC求：AB及OC的长．12．已知：⊙O中，OC⊥AB于C点，AB＝16cm，53sinAOC(1)求⊙O的半径OA的长及弦心距OC；(2)求cos∠AOC及tan∠AOC．13．已知：如图，△ABC中，AC＝12cm，AB＝16cm，31sinA(1)求AB边上的高CD；(2)求△ABC的面积S；(3)求tanB．14．已知：如图，△ABC中，AB＝9，BC＝6，△ABC的面积等于9，求sinB．拓展、探究、思考15．已知：如图，Rt△ABC中，∠C＝90°，按要求填空：(1),sincaA∴cAca,sin______；(2),coscbA∴b＝______，c＝______；(3),tanbaA∴a＝______，b＝______；(4),23sinB∴Bcos______，Btan______；(5),53cosB∴Bsin______，Atan______；(6)∵Btan3，∴Bsin______，Asin______．