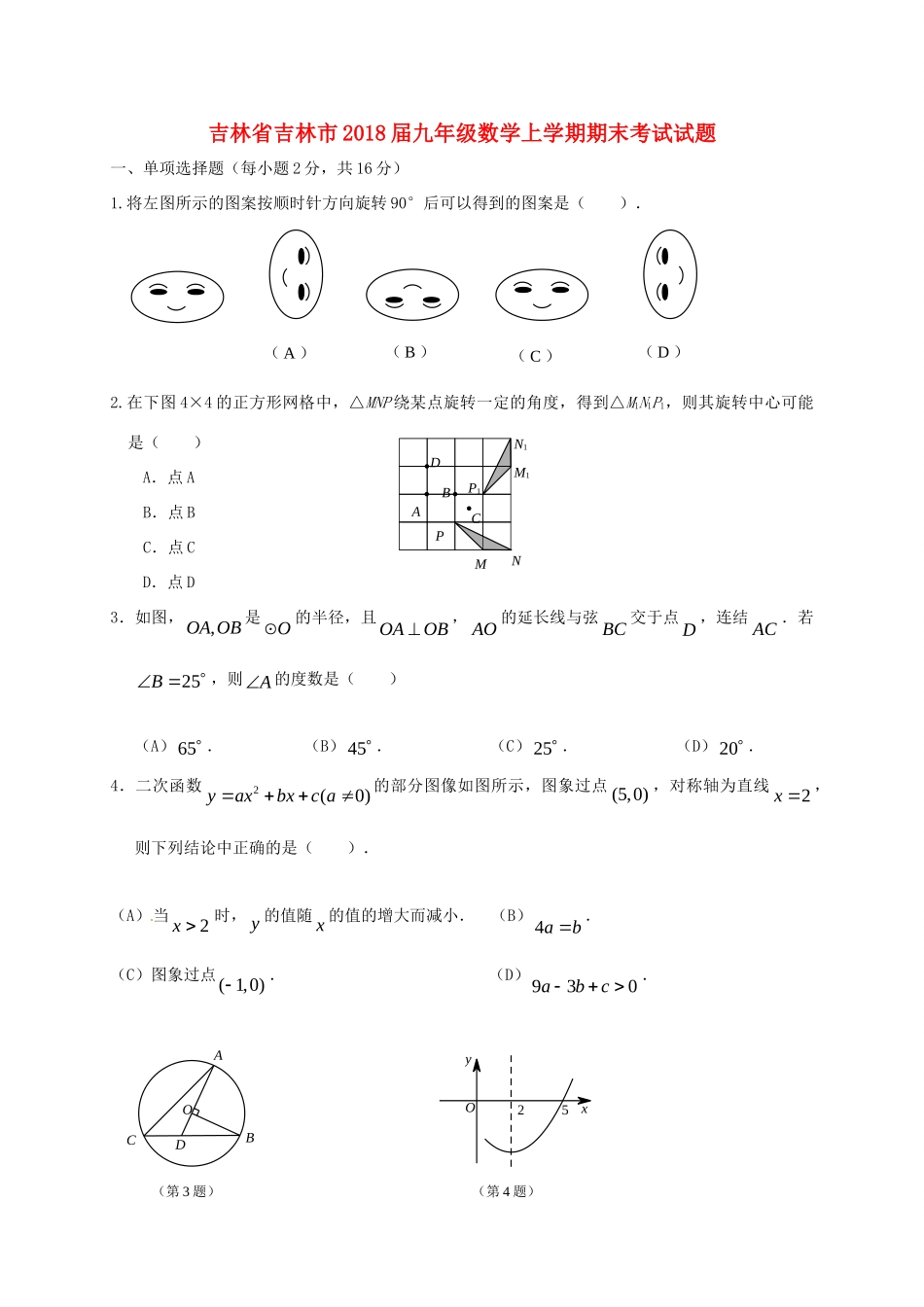
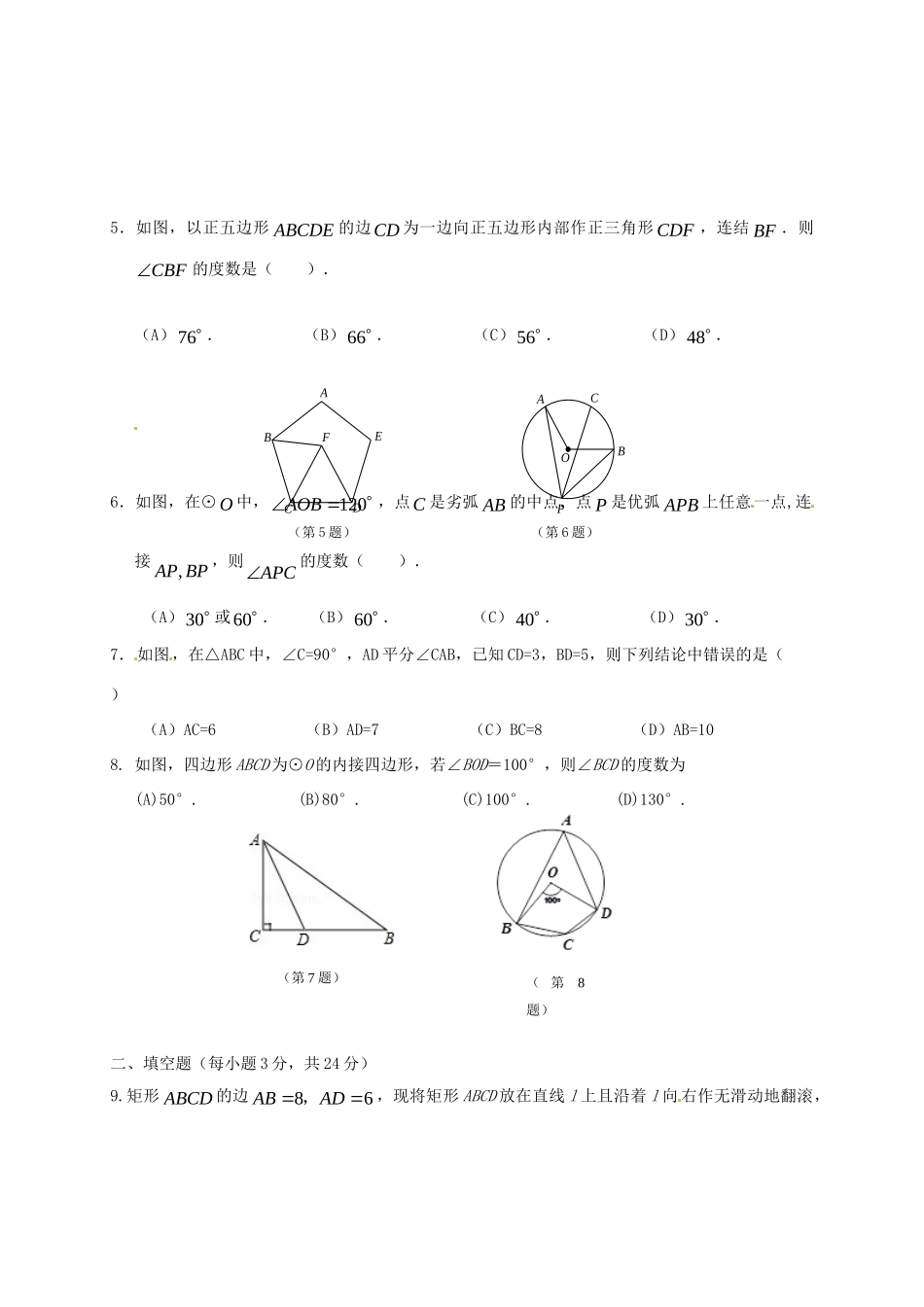
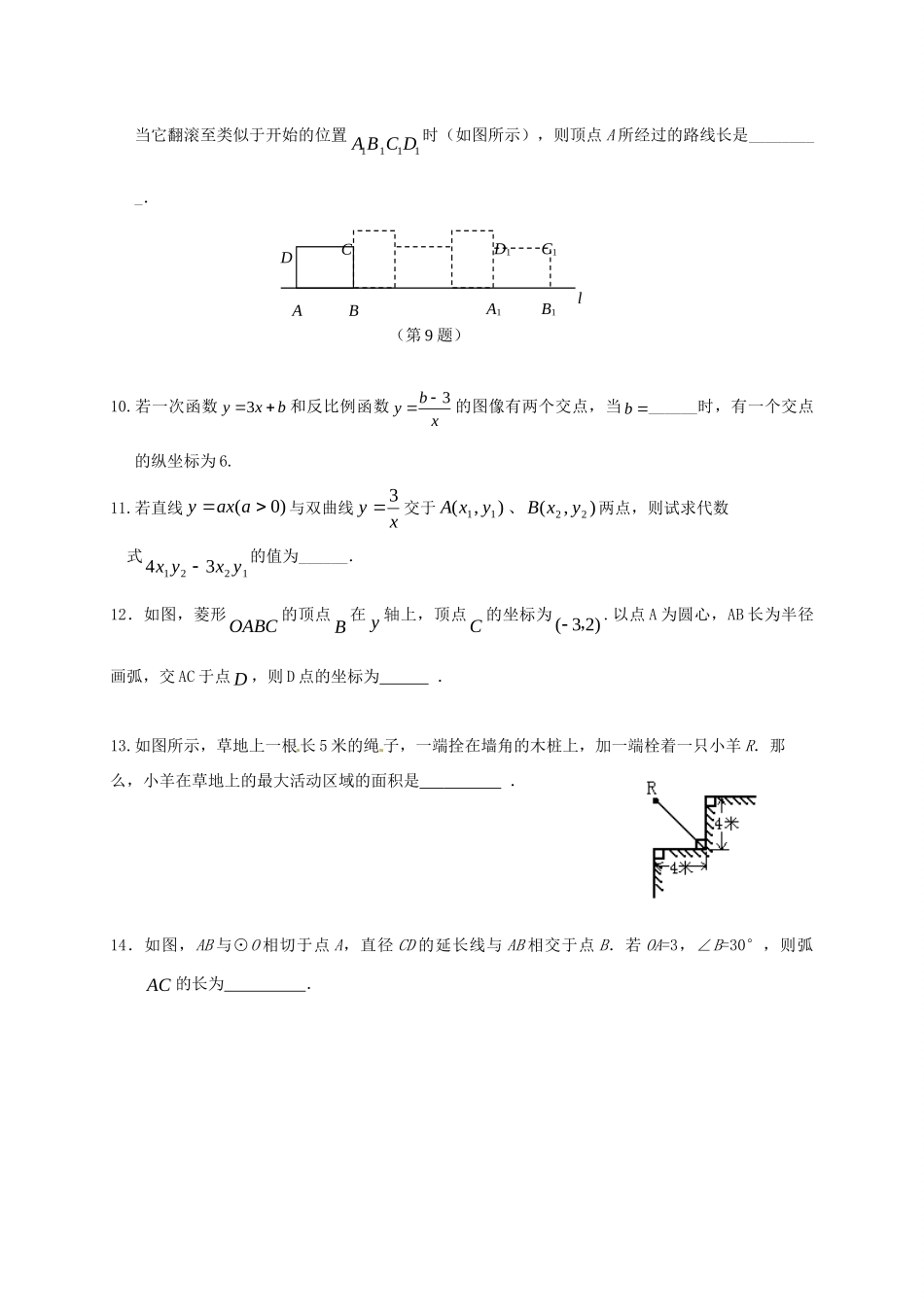
吉林省吉林市2018届九年级数学上学期期末考试试题一、单项选择题(每小题2分,共16分)1.将左图所示的图案按顺时针方向旋转90°后可以得到的图案是().2.在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是()A.点AB.点BC.点CD.点D3.如图,,OAOB是O的半径,且OAOB,AO的延长线与弦BC交于点D,连结AC.若25B,则A的度数是()(A)65.(B)45.(C)25.(D)20.4.二次函数2(0)yaxbxca的部分图像如图所示,图象过点(5,0),对称轴为直线2x,则下列结论中正确的是().(A)当2x时,y的值随x的值的增大而减小.(B)4ab.(C)图象过点(1,0).(D)930abc.(第3题)(第4题)25xyOODCBA(A)(B)(C)(D)ABCDMNPP1M1N15.如图,以正五边形ABCDE的边CD为一边向正五边形内部作正三角形CDF,连结BF.则CBF的度数是().(A)76.(B)66.(C)56.(D)48.6.如图,在⊙O中,120AOB,点C是劣弧AB的中点.点P是优弧APB上任意一点,连接,APBP,则APC的度数().(A)30或60.(B)60.(C)40.(D)30.7.如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是()(A)AC=6(B)AD=7(C)BC=8(D)AB=108.如图,四边形ABCD为⊙O的内接四边形,若∠BOD=100°,则∠BCD的度数为(A)50°.(B)80°.(C)100°.(D)130°.二、填空题(每小题3分,共24分)9.矩形ABCD的边86ABAD,,现将矩形ABCD放在直线l上且沿着l向右作无滑动地翻滚,PAOCBFEDCBA(第5题)(第6题)(第7题)(第8题)当它翻滚至类似于开始的位置1111ABCD时(如图所示),则顶点A所经过的路线长是_________.10.若一次函数3yxb和反比例函数3byx的图像有两个交点,当b______时,有一个交点的纵坐标为6.11.若直线)0(aaxy与双曲线xy3交于),(11yxA、),(22yxB两点,则试求代数式122134yxyx的值为______.12.如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(32),.以点A为圆心,AB长为半径画弧,交AC于点D,则D点的坐标为.13.如图所示,草地上一根长5米的绳子,一端拴在墙角的木桩上,加一端栓着一只小羊R.那么,小羊在草地上的最大活动区域的面积是.14.如图,AB与⊙O相切于点A,直径CD的延长线与AB相交于点B.若OA=3,∠B=30°,则弧AC的长为.DCABA1B1C1D1l(第9题)15.关于x的方程kx2﹣4x﹣23=0有实数根,则k的取值范围是.16.如图,在矩形ABCD中,AB=8,BC=12,E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=.三、解答题(共20分)17用配方法解方程:2210xx(满分5分)18用分解因式法解方程:2450xx(满分5分)19.(本小题满分5分)某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,求每年投资的增长率.20.(本小题满分5分)在一个不透明的袋子里装有4个小球,分别标有数字1,2,3,4,这些小球除所标数字不同外其余均相同.先从袋子里随机摸出1个小球,记下标号后不放回;再从袋子(第12题)yxDCBAOABCOD(第14题)里随机摸出1个小球记下标号.请用画树形图(或列表)的方法,求两次摸出的小球的标号之和是5的概率.四、解答题(每小题7分,共14分)21.如图,在直角坐标系xOy中,一次函数1ykxb的图像与反比例函数2kyx的图像交于143ABm,,,两点.(1)求一次函数的解析式;(2)求AOB的面积.22.水平地面上的甲、乙两楼的距离为30米,从甲楼的顶部测得乙楼顶部的仰角为30°,测得乙楼底部的俯角为45°.(1)请你画出测量示意图(大楼的长、宽忽略不计);(2)求甲、乙两楼的高度.(结果精确到0.1m,3=1.73)五、解答题(每小题8分,共16分)(第22题)B(3,m)A(1,4)xyO23.(本小题满分8分)已知反比例函数5myx(m为常数,且m≠5).(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围.;(2)若其图象与一次函数y=﹣x+1...