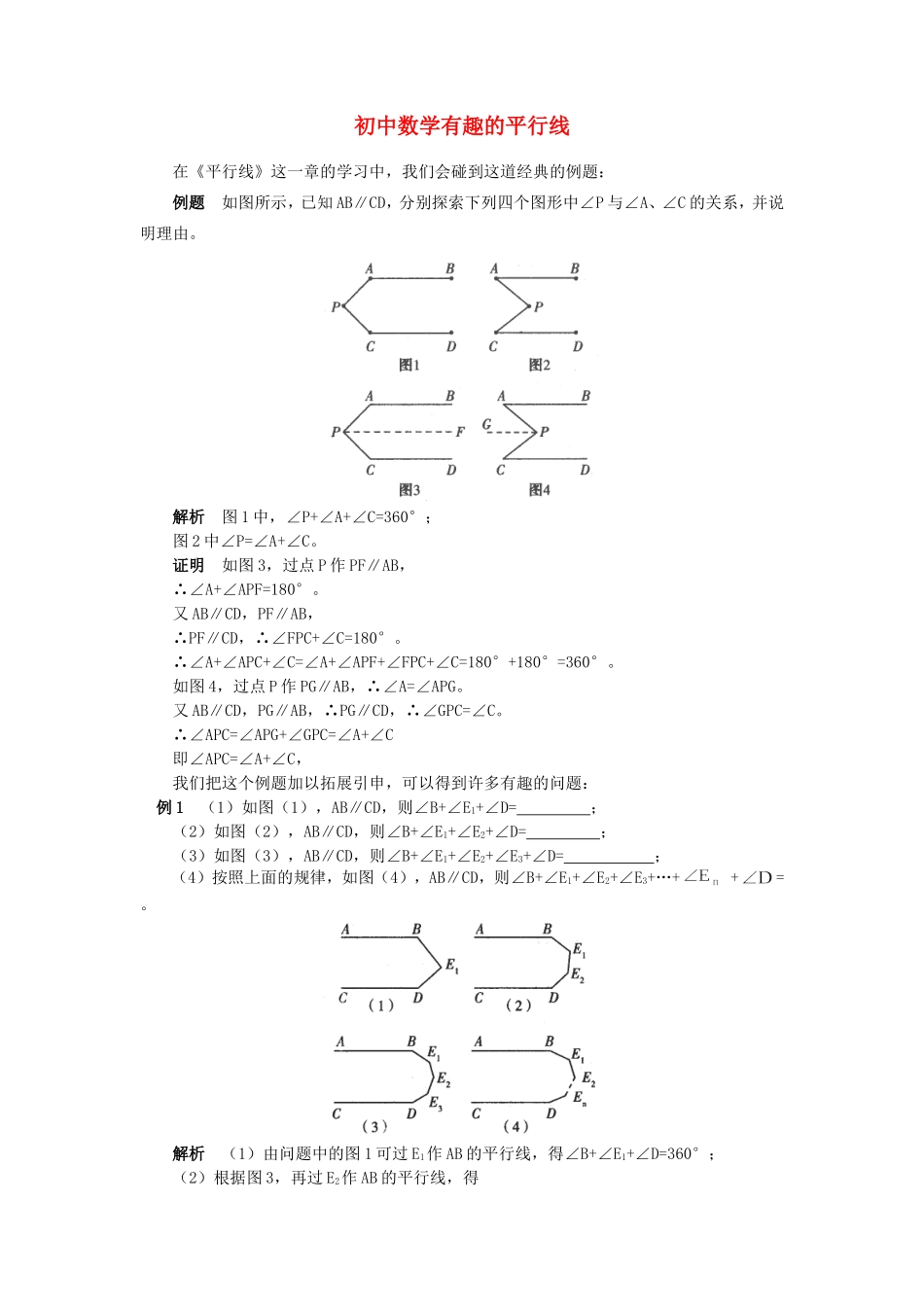
初中数学有趣的平行线在《平行线》这一章的学习中,我们会碰到这道经典的例题:例题如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A、∠C的关系,并说明理由。解析图1中,∠P+∠A+∠C=360°;图2中∠P=∠A+∠C。证明如图3,过点P作PF∥AB,∴∠A+∠APF=180°。又AB∥CD,PF∥AB,∴PF∥CD,∴∠FPC+∠C=180°。∴∠A+∠APC+∠C=∠A+∠APF+∠FPC+∠C=180°+180°=360°。如图4,过点P作PG∥AB,∴∠A=∠APG。又AB∥CD,PG∥AB,∴PG∥CD,∴∠GPC=∠C。∴∠APC=∠APG+∠GPC=∠A+∠C即∠APC=∠A+∠C,我们把这个例题加以拓展引申,可以得到许多有趣的问题:例1(1)如图(1),AB∥CD,则∠B+∠E1+∠D=;(2)如图(2),AB∥CD,则∠B+∠E1+∠E2+∠D=;(3)如图(3),AB∥CD,则∠B+∠E1+∠E2+∠E3+∠D=;(4)按照上面的规律,如图(4),AB∥CD,则∠B+∠E1+∠E2+∠E3+…++=。解析(1)由问题中的图1可过E1作AB的平行线,得∠B+∠E1+∠D=360°;(2)根据图3,再过E2作AB的平行线,得∠B+∠E1+∠E2+∠D=360°+180°=540°;(3)依次类推,得∠B+∠E1+∠E2+∠E3+∠D=540°+180°=720°;(4)∠B+∠E1+∠E2+∠E3+…+∠En+∠D=(n+1)·180。例2(1)如图(1),AB∥CD,则∠E1与∠B、∠D的关系是;(2)如图(2),AB∥CD,则∠E1+∠E2与∠B、∠D的关系是;(3)如图(3),AB∥CD,则∠E1+∠E2+∠E3与∠B、∠D的关系是;(4)按照上面的规律,如图(4),AB∥CD,则∠E1+∠E2+∠E3+…+∠En与∠B、∠D的关系是。解析(1)由问题中的图4可证得∠E1=∠B+∠D;(2)根据图4,再过E2作AB的平行线,得∠E1+∠E2=∠B+∠D+180°;(3)依次类推,得∠E1+∠E2+∠E3=∠B+∠D+360°;(4)∠E1+∠E2+∠E3+…+∠En=∠B+∠D+(n-1)·180°。例3(1)如图(1),AB∥CD,BE1平分∠ABE,DE1平分∠CDE,∠BED=150°。那么∠E1=;(2)如图(2),AB∥CD,BE1平分∠ABE,DE1平分∠CDE,BE2平分∠ABE1,DE2平分∠CDE1,则∠E2=;(3)如图(3),AB∥CD,BE1平分∠ABE,DE1平分∠CDE,BE2平分∠ABE1,DE2平分∠CDE1,BE3平分∠ABE2,DE3平分∠CDE2,则∠E3=;(4)按照上面的规律,如图(4),AB∥CD,BE1平分∠ABE,DE1平分∠CDE,BE2平分∠ABE1,DE2平分∠CDE1,BE3平分∠ABE2,DE3平分∠CDE2,BE3平分∠ABE2,DE3平分∠CDE2…,则∠En=。解析(1)由问题中的图2可得∠E=∠ABE+∠EDC,∠BED=150°,∴∠ABE+∠EDC=150°;同理∠E1=∠ABE1+∠E1DC=(2)∠E2==37.5°。(3)∠E3==18.25°。(4)∠En=。例4(1)如图(1),若AB∥CD,则∠B+∠C=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?请说明理由;(3)若将点E移至图(2)所示位置,此时∠B、∠D、∠E之间有什么关系?请说明理由;(4)若将点E移至图(3)所示位置,情况又如何?(5)在图(4)中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?解析(1)由问题中的图4可证得∠E=∠B+∠D。(2)当∠B+∠D=∠E时,直线AB与CD平行。证明如下:过点E作EF∥AB,则∠B=∠BEF。又∠B+∠D=∠BED,∴∠D=∠DEF,∴EF∥CD,∴AB∥EF∥CD即AB∥CD。(3)∠B+∠D+∠E=360°(过点E作EF∥AB,方法同上)。(4)∠B=∠D+∠E。(5)∠E+∠G=∠B+∠F+∠D。