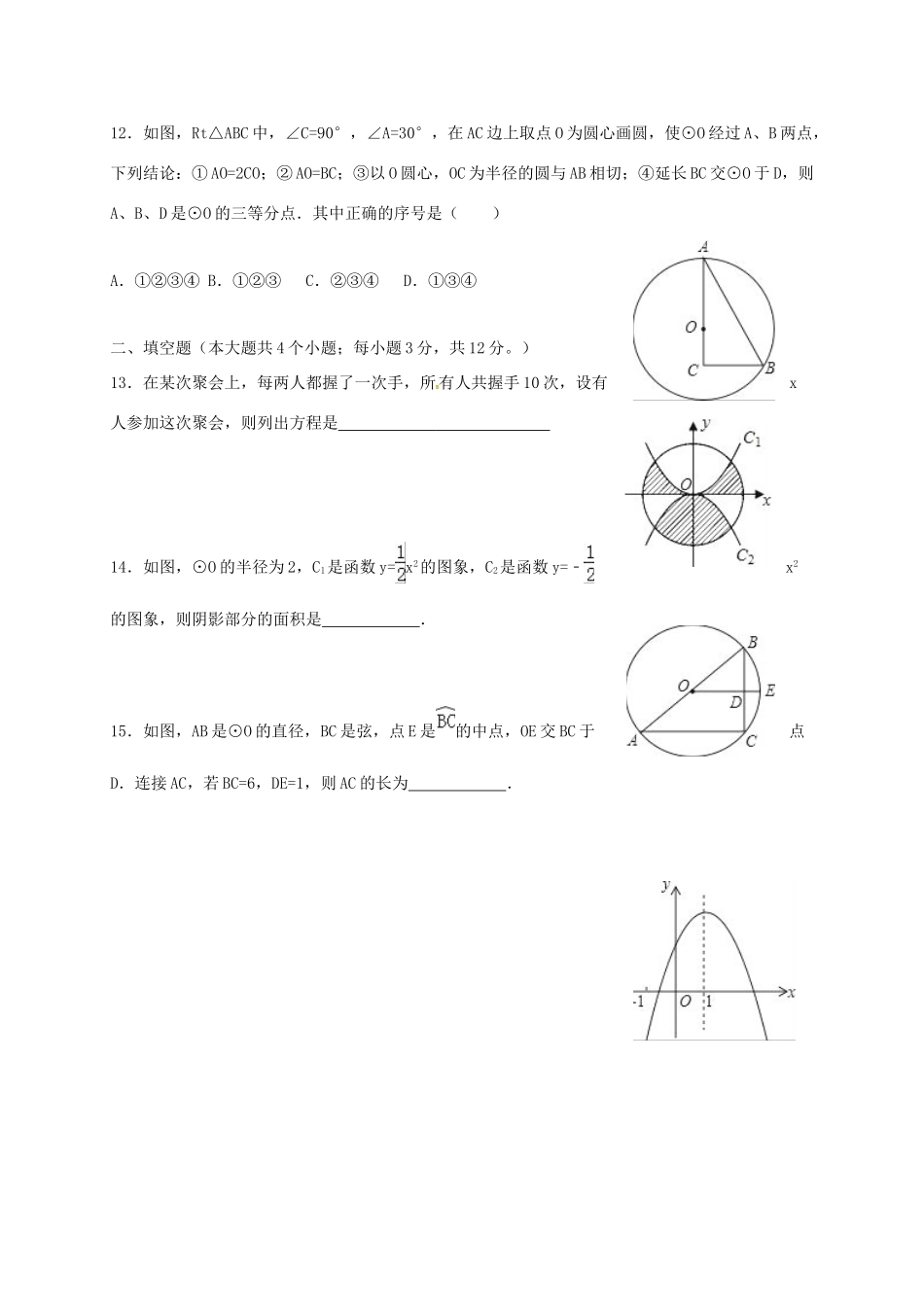
内蒙古翁牛特旗乌丹镇2018届九年级数学上学期12月月考试题一、选择题(本大题共12个小题,每小题3分,共36分。)1.抛物线y=(x﹣2)2+4的顶点坐标是()A.(2,﹣4)B.(﹣2,4)C.(﹣2,﹣4)D.(2,4)2.如图,下列四种标志中,既是轴对称图形又是中心对称图形的为()A.B.C.D.3.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为2的圆与OA的位置关系是()A.相离B.相交C.相切D.以上三种情况均有可能4.将抛物线y=2(x﹣4)2﹣1如何平移可得到抛物线y=2x2()A.向左平移4个单位,再向上平移1个单位B.向左平移4个单位,再向下平移1个单位C.向右平移4个单位,再向上平移1个单位D.向右平移4个单位,再向下平移1个单位5.若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是()A.k>﹣1B.k>﹣1且k≠0C.k<1D.k<1且k≠06.如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度为()A.1cmB.2cmC.3cmD.4cm7.已知一个三角形的两边长是方程x2﹣8x+15=0的两根,则第三边y的取值范围是()A.y<8B.3<y<5C.2<y<8D.无法确定8.如图:已知⊙P的半径为1,圆心P在抛物线y=上运动,当⊙P与x轴相切时,圆心P的坐标为()A.(﹣2,1)B.(2,1)C.(0,﹣1)D.(﹣2,1)或(2,1)或(0,﹣1)9.在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是()A.点AB.点BC.点CD.点D10.如图,AB为⊙O的一固定直径,它把⊙O分成上,下两个半圆,自上半圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A,B两点)上移动时,点P()A.到CD的距离保持不变B.位置不变C.等分D.随C点移动而移动11.一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣x2+x+.则他将铅球推出的距离是()m.A.8B.9C.10D.1112.如图,Rt△ABC中,∠C=90°,∠A=30°,在AC边上取点O为圆心画圆,使⊙O经过A、B两点,下列结论:①AO=2CO;②AO=BC;③以O圆心,OC为半径的圆与AB相切;④延长BC交⊙O于D,则A、B、D是⊙O的三等分点.其中正确的序号是()A.①②③④B.①②③C.②③④D.①③④二、填空题(本大题共4个小题;每小题3分,共12分。)13.在某次聚会上,每两人都握了一次手,所有人共握手10次,设有x人参加这次聚会,则列出方程是14.如图,⊙O的半径为2,C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是.15.如图,AB是⊙O的直径,BC是弦,点E是的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为.16.已知二次函数y=ax2+bx+c的图象如图所示,结论①a+b+c>0;②a﹣b+c<0;③abc<0;④b=2a;⑤b>0,其中结论错误的是(填序号).三、解答题(本大题共10个小题,共102分.解答应写出文字说明、证明过程或演算步骤)17.(6分)解方程:x(x﹣5)+x﹣5=0.18.(8分)已知关于x的一元二次方程(m+1)x2-x+m2-3m-3=0有一个根是1,求m的值及另一根.19.(10分)如图,四边形ABCD内接于⊙O,AD∥BC,求证:AB=CD.20.(12分)某如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.(1)求证:BC是⊙O的切线;(2)已知∠B=30°,CD=4,求线段AB的长.21.(10分)已知,如图,点C是AB上一点,分别以AC,BC为边,在AB的同侧作等边三角形△ACD和△BCE.(1)指出△ACE以点C为旋转中心,顺时针方向旋转60°后得到的三角形;(2)若AE与BD交于点O,求∠AOD的度数.22.(10分)如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(﹣1,2).(1)画出△ABC绕点D(0,5)逆时针旋转90°后的△A1B1C1;并标出A1,B1,C1的坐标.(2)画出△ABC关于原点O的中心对称图形△A2B2C2,并标出A2,B2,C2的坐标.23.(12分)水果批发商场经销一种水果,如果每千克盈利5元,每天可售出200千克,经市场调查发现,在进价不变的情况下,若...