九年级数学一模试卷(pdf，无答案)试卷VIP免费

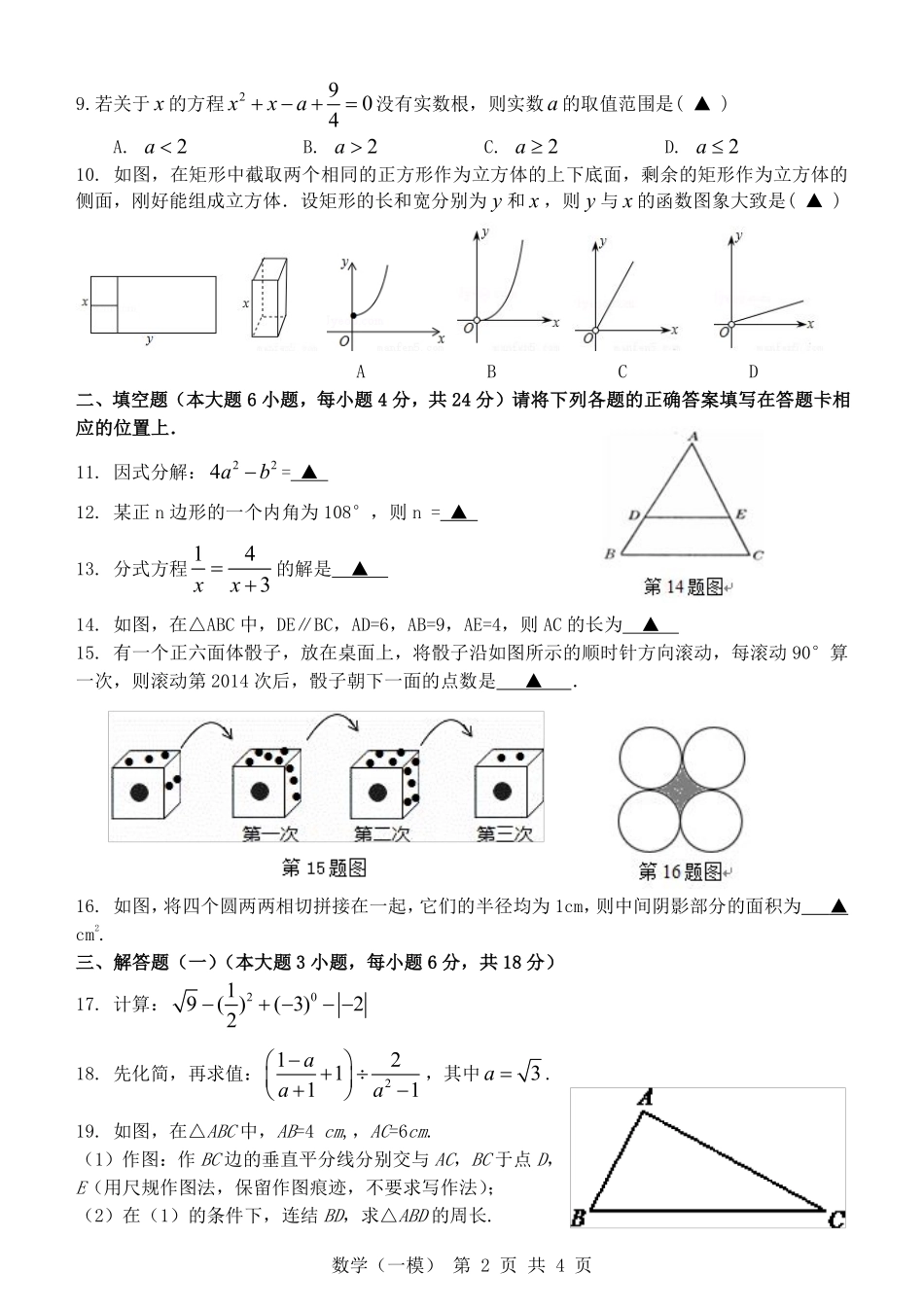
数学（一模）第1页共4页封开县中小学教学目标管理2016年初中毕业班第一次模拟题数学说明：全卷共4页，考试时间为100分钟，满分120分．一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1.2016-=(▲)A.2016B.-2016C.12016D.12016-2.某小区居民王先生改进用水设施，在5年内帮助他居住小区的居民累计节水39400吨，将39400用科学计数法表示应为(▲)A.3.9×104B.3.94×104C.39.4×103D.4.0×1043.一组数据12，16，5，22，4，则这组数据的中位数是(▲)A.5B.12C.16D.224.()22ab-=（▲）A.4ab-B.4abC.224abD.24ab5.在0，2，3，()05-这四个数中，最大的数是(▲)A.0B.2C.3D.()05-6.如图，AD∥BC，∠B=30°，DB平分∠ADE，则∠DEC的度数为(▲)A.30°B.60°C.90°D.120°7.下列图形中，既是轴对称图形又是中心对称图形的是(▲)ABCD8.如图四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B=135°，则的长是(▲)A.2B.C.2D.3题号一二三四五总分171819202122232425得分第6题图AC数学（一模）第2页共4页9.若关于x的方程2904xxa没有实数根，则实数a的取值范围是(▲)A.2aB.2aC.2aD.2a10.如图，在矩形中截取两个相同的正方形作为立方体的上下底面，剩余的矩形作为立方体的侧面，刚好能组成立方体．设矩形的长和宽分别为y和x，则y与x的函数图象大致是(▲)ABCD二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11.因式分解：224ab=▲12.某正n边形的一个内角为108°，则n=▲13.分式方程143xx的解是▲14.如图，在△ABC中，DE∥BC，AD=6，AB=9，AE=4，则AC的长为▲15.有一个正六面体骰子，放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，则滚动第2014次后，骰子朝下一面的点数是▲．16.如图，将四个圆两两相切拼接在一起，它们的半径均为1cm，则中间阴影部分的面积为▲cm2.三、解答题（一）（本大题3小题，每小题6分，共18分）17.计算：2019()(3)2218.先化简，再求值：212111aaa，其中3a.19.如图，在△ABC中，AB=4cm,，AC=6cm.（1）作图：作BC边的垂直平分线分别交与AC，BC于点D，E（用尺规作图法，保留作图痕迹，不要求写作法）；（2）在（1）的条件下，连结BD，求△ABD的周长.数学（一模）第3页共4页四、解答题（二）（本大题3小题，每小题7分，共21分）20.如图，由山脚下的一点A测得山顶D的仰角是30°，从A前进100米到B，再次测得山顶D的仰角为60°，求山高CD的高度（结果精确到0.1米）。（参考数据：2≈1.414，3≈1.732）21.如图，点E为矩形ABCD外一点，AE=DE，连接EB、EC分别与AD相交于点F、G．求证：（1）△EAB≌△EDC；（2）∠EFG=∠EGF．22.为了解中考体育科目训练情况，某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：（1）求本次抽样测试的学生人数；（2）求出C级的学生人数，并把条形统计图补充完整；（3）测试老师想从4位同学（分别记为E、F、G、H，其中E为小明）中随机选择两位同学了解平时训练情况，请用列表或画树形图的方法求出选中小明的概率．数学（一模）第4页共4页五、解答题（三）（本大题3小题，每小题9分，共27分）23.如图，直线yxb与双曲线myx都经过点A（2，3），直线yxb与x轴、y轴分别交于B、C两点．（1）求直线和双曲线的函数解析式；（2）求△AOB的面积．24.如图，已知在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．连接CD.（1）求证：PA是⊙O的切线；（2）过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG•AB=12，求AC的长；（3）在满足（2）的条件下，若AF：FD=1：2，GF=1，求⊙O的半径及sin∠ACE的值．25.如图，在矩形ABCD中，AB=3cm，BC=4cm．设P，Q分别为BD，BC上的动点，点P自点D沿DB方向作匀速移动的同时，点Q自点B沿BC方向向点C作匀速移动，移动的速度均为1cm/s，设P，Q移动的时间为t（0≤t≤4）．（1）当t为何值时，PQ⊥BC；（2）写出△PBQ的面积S（cm2）与时间t（s）之间的函数表达式，当t为何值时，S有最大值？最大值是多少；（3）当t为何值时，△PBQ为等腰三角形.