九年级数学解直角三角形山东教育版知识精讲试卷VIP免费

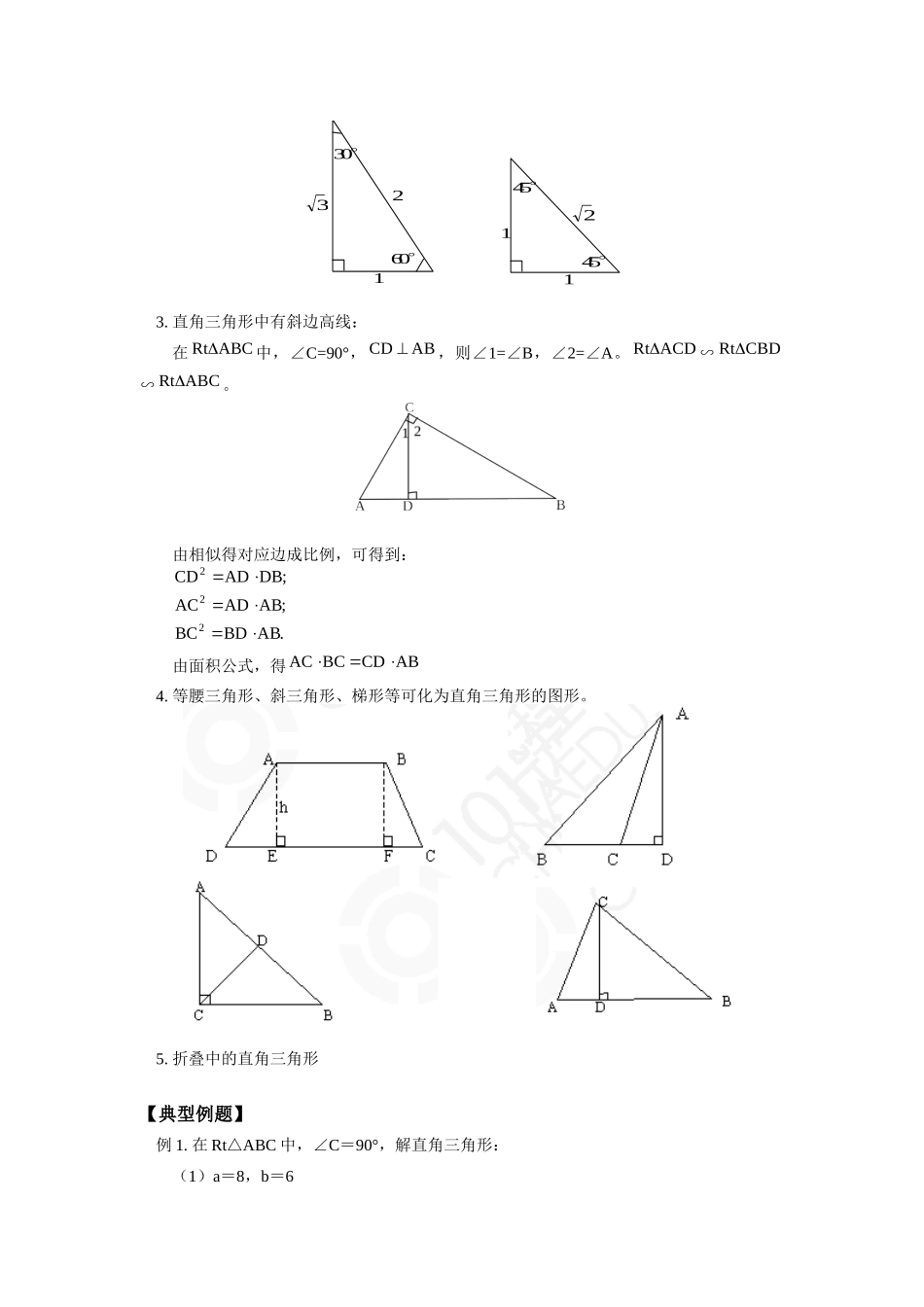
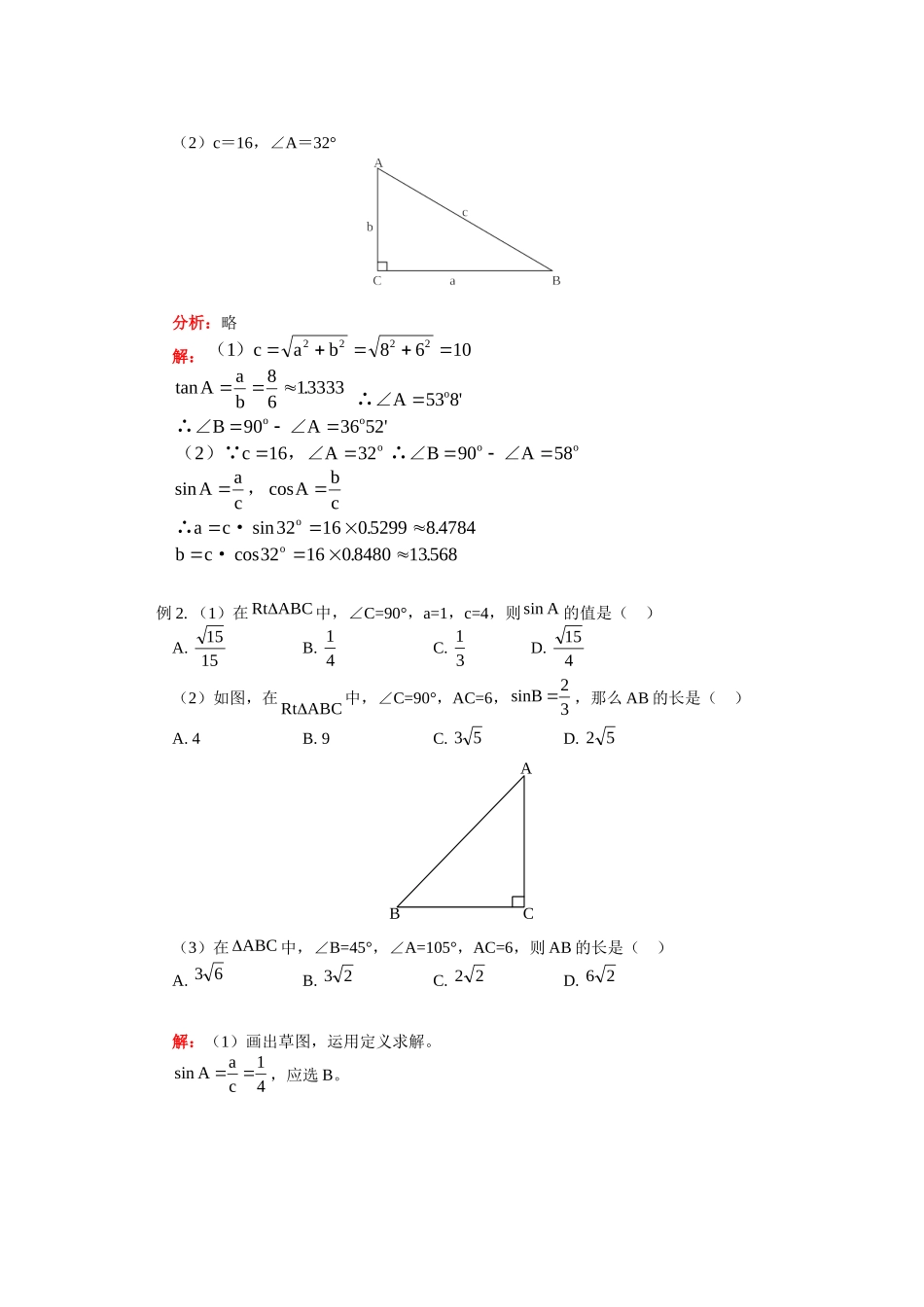
九年级数学解直角三角形山东教育版【本讲教育信息】一.教学内容：解直角三角形二.教学重难点：1.解直角三角形的理论依据。（1）在ABCtR中，∠C=90°①两锐角互余——∠A+∠B=90°②三边关系——勾股定理：222cba，变式③边、角关系——锐角三角函数：邻边对边，斜边邻边，斜边对边tanAcosAAsin。已知直角三角形的两个基本元素（至少有一个是边），利用以上关系就可以求出其余的未知元素，其中恰当地选用边角关系是关键。应注意以下原则：（1）有“斜”选“弦”，无“斜”选“切”。（2）尽量使未知元素在分子的位置上，以便利用乘法运算求未知元素。（3）尽量使用原始数据：以减少误差的积累，也可避免由于中间数据有错而产生新的误差。2.特殊的直角三角形：①含30°角的直角三角形：在ABCtR中，∠C=90°，∠A=30°，则AB21BC,60B，三边之比为2:3:1。②含45°角的直角三角形：在ABCtR中，∠C=90°，∠A=45°，则∠B=45°，AC=BC,三边之比为2:1:1。32160°30°45°45°1123.直角三角形中有斜边高线：在ABCtR中，∠C=90°，ABCD，则∠1=∠B，∠2=∠A。ACDtR∽CBDRt∽ABCRt。由相似得对应边成比例，可得到：.ABBDBC;ABADAC;DBADCD222由面积公式，得ABCDBCAC4.等腰三角形、斜三角形、梯形等可化为直角三角形的图形。5.折叠中的直角三角形【典型例题】例1.在Rt△ABC中，∠C＝90°，解直角三角形：（1）a＝8，b＝6（2）c＝16，∠A＝32°分析：略解：（）186102222cabtan.Aab8613333∴∠Ao538'∴∠∠BAoo903652'（） ，∠21632cAo∴∠∠BAoo9058sincosAacAbc，∴·acosin..32160529984784bco·cos..32160848013568例2.（1）在ABCRt中，∠C=90°，a=1，c=4，则Asin的值是（）A.1515B.41C.31D.415（2）如图，在ABCRt中，∠C=90°，AC=6，32sinB，那么AB的长是（）A.4B.9C.53D.52ABC（3）在ABC中，∠B=45°，∠A=105°，AC=6，则AB的长是（）A.63B.23C.22D.26解：（1）画出草图，运用定义求解。41caAsin，应选B。注意：正确运用三角函数定义求解。（2）6AC,32Bsin,ABACBsin，9ABAB632应选B。（3）画出草图，进行分析，45°要起作用，须放入Rt，作高构造Rt求解。作BCAD于D，则∠1=45°，∠2=60°，∠C=30°3AD6AC在ABDRt中，∠B=45°，23AD2AB应选B。例3.如图，在ABC中，32AC,23Btan,23Acos，求AB的长。分析：由23Acos，得∠A=30°，要使30°角，23Btan起作用，则需构造Rt。解：作ABCD于D在ACDRt中，32332AcosACAD,3CD,30A32AC,23Acos在BCDRt中，523BDADAB2BD3CDCD2BD3,23BDCD23Btan又注意：①特殊角，锐角三角函数值要放在Rt中应用；②求一条线段的长，也可以根据需要分段求和。例4.梯形ABCD中，AB//CD，45D,60C,3213CD,11AB。求这个梯形的周长和面积。解析：可通过设未知数并转化成三角形和矩形来求解。（如图）作hAE,FCDBF,ECDAE设于于则45D,ADERt中32h,321311h)133(3213DEEFCFCDh332BC,h33CF60C,hBF,BCFRth2AD,hDEAE解方程得中又4BC,62AD。326228DACDBCABL周长面积632432)321311(21)CDAB(AE21SABCD（注：等腰三角形，平行四边形，菱形等的求解问题也可通过作高线等方法使其转化到直角三角形中去求解。）例5.如图，在ABCRt中，∠B=90°，∠A=30°，AC=3，将BC向BA方向折过去，使点C落在BA上的C′点，折痕为BE，求E'C的长。分析：由图形折叠知E'BCBCE得4521,CEE'C在BEC中，∠EBC=45°，∠C=60°由例2的（3）想一想你该如何求解解：作BCED于D在ABCRt中，∠ABC=90°，∠A=30°，AC=3,23AC21BC∠C=60°在CEDRt中，∠EDC=90°，∠DEC=30°EC21DC设DC=x，则EC=2x，DE=x3在BDERt中，∠EDB=90°，∠1=45°2)13(3'2)13(3)13)(13()13(31332)13(23x,23)13(,2333...