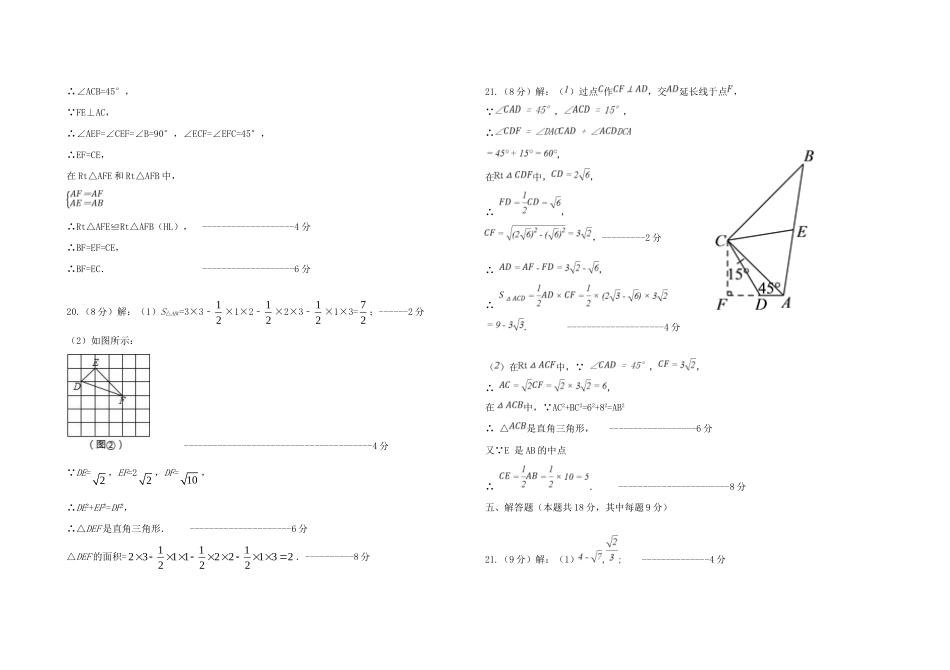
江西省南昌市初中十校2017-2018学年八年级数学下学期期中联考试题答案一、选择题(3分×8=24分)1.A2.D3.D4.A5.C6.A7.C8.D二、填空题(3分×6=18分)9.x≥-110.1811.12.(2,2)13.①②④14.510.2或三、计算题(每小题4分,共8分)15.(1)解原式=3﹣2+﹣3-----------------2分=﹣;----------------------------------4分()原式---------------2分.----------------------------------------4分16.(6分)解:原式=(2221111xxx+)•221xx+,=211xxx+•221xx+,=11xx+,-------------------3分当x=2+1时,原式=1+2.-----------------6分四、解答题(共34分,其中第17-19题每题6分,第20、21题每题8分)17、(6分)(1)在Rt△ABD中,AD=222254ABBD=3;------3分(2)在Rt△ACD中,AC=22223312ADCD=23,------4分则△ABC的周长=AB+AC+BC=5+4+3+23=9+33.----------------6分18.(6分)解:∵四边形ABCD是平行四边形,∴AB=DC,AD=BC,OA=OC,OB=OD.∵△BOC的周长比△AOB的周长小3cm,∴(AB+OB+OA)-(BC+OC+OB)=3,∴AB-BC=3.---------------------------------------------------2分∵2(AB+BC)=26,∴AB+BC=13,-------------------------------------------------4分∴AB=8cm,BC=5cm.-----------------------------------------------6分19、(6分)解:如图连接AF.∵四边形ABCD是正方形,∴∠ACB=45°,∵FE⊥AC,∴∠AEF=∠CEF=∠B=90°,∠ECF=∠EFC=45°,∴EF=CE,在Rt△AFE和Rt△AFB中,∴Rt△AFE≌Rt△AFB(HL),-------------------4分∴BF=EF=CE,∴BF=EC.-------------------6分20.(8分)解:(1)S△ABC=3×3﹣12×1×2﹣12×2×3﹣12×1×3=72;------2分(2)如图所示:---------------------------------------4分∵DE=2,EF=22,DF=10,∴DE2+EF2=DF2,∴△DEF是直角三角形.---------------------6分△DEF的面积=111231122132222.----------8分21.(8分)解:()过点作,交延长线于点,∵,,∴,在中,,∴,,---------2分∴,∴.--------------------4分()在中,∵,,∴,在中,∵AC2+BC2=62+82=AB2∴△是直角三角形,------------------6分又∵E是AB的中点∴.-----------------------8分五、解答题(本题共18分,其中每题9分)21.(9分)解:(1),;--------------4分(2)10--------------6分(3)原式===10-1=9.-------------------9分22.(9分)解:(1)∵四边形ABCD是矩形,∴AB=CD,AB∥CD,AD∥BC,∠B=90°,∴AC=10,∠GAF=∠HCE,------------------2分∵G,H分别是AB,DC中点,∴AG=BG,CH=DH,∴AG=CH,∵AE=CF,在△AFG和△CEH中,{AGCHGAFHCEAFCE∴△AFG≌△CEH(SAS),∴GF=HE,同理:GE=HF,∴四边形EGFH是平行四边形.-----------------5分(2)由(1)得:BG=CH,BG∥CH,∴四边形BCHG是平行四边形,∴GH=BC=8,当EF=GH=8时,平行四边形EGFH是矩形,分两种情况:①AE=CF=t,EF=10﹣2t=8,解得:t=1;------------------7分②AE=CF=t,EF=10﹣2(10﹣t)=8,解得:t=9;--------9分综上所述:当t为1s或9s时,四边形EGFH为矩形.六、解答题(本题12分)24.(12分)解:①是;------------------------------------2分②设,CDx根据勾股定理可得:22224,1CBCDCACD,于是222413CDCDCD,∴3CD;--------------------5分●深入探究由222CACBCD可得:222CACDCB,而222CACDAD,∴22ADCB,即ADCB;---------------8分●推广应用过点A向ED引垂线,垂足为G,∵“勾股高三角形”△ABC为等腰三角形,且ABACBC,∴只能是222ACBCCD,由上问可知ADBC……①.又ED∥BC,∴1B……②.而90AGDCDB……③,∴△AGD≌△CDB(AAS),于是DGBD.易知△ADE与△ABC均为等腰三角形,根据三线合一原理可知22EDDGBD.又,,ABACADAE∴BDECa,∴2EDa.------------------------12分A1BDECGG