九年级数学上学期第一次(10月)月考试卷 苏科版试卷VIP免费

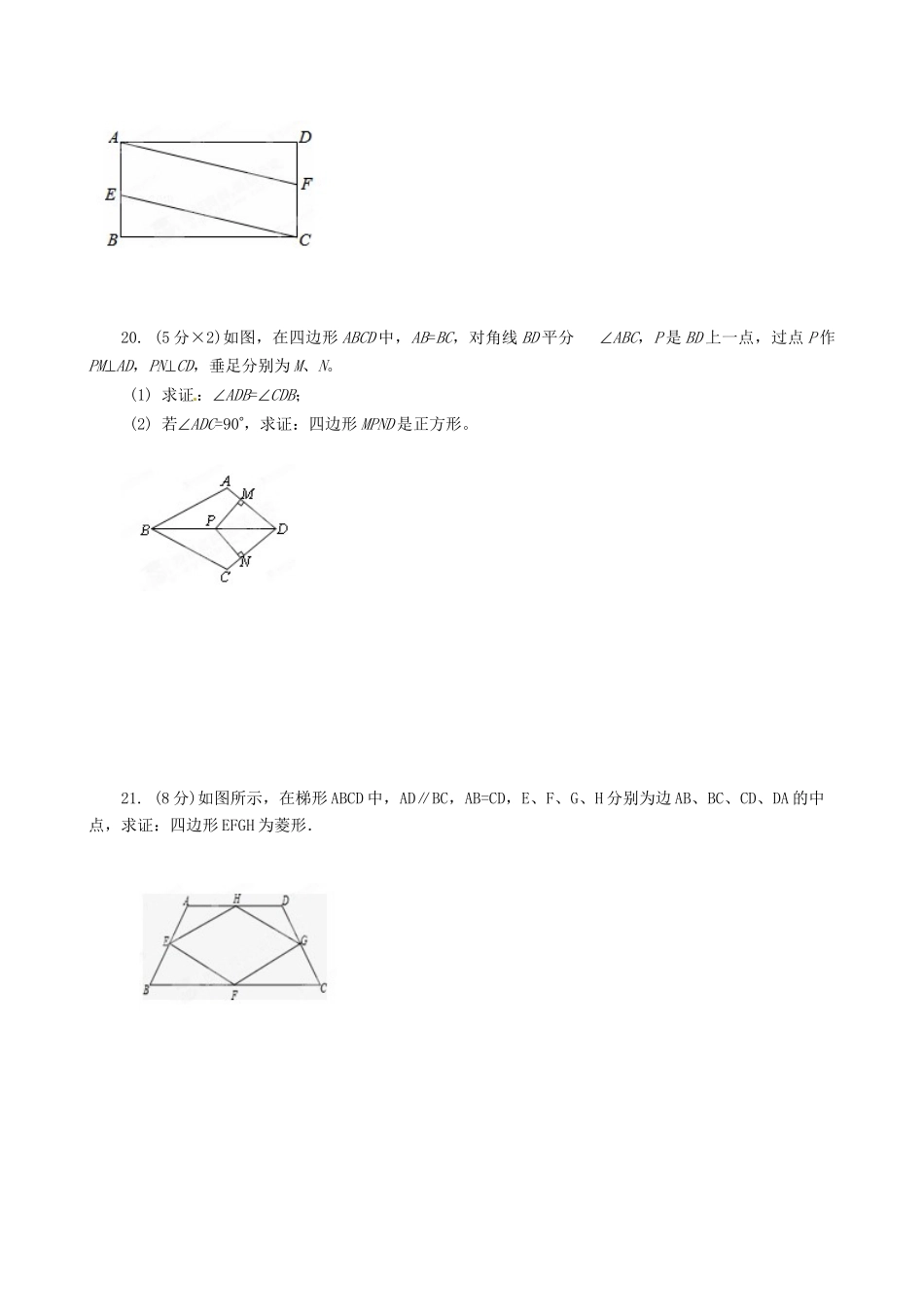
江苏省兴化市安丰初级中学2014届九年级上学期第一次（10月）月考数学试题（暂无答案）苏科版成绩：＿＿＿＿＿＿＿一选择题:(3分×6)题号123456答案1．等腰三角形两边长分别为4和8，则这个等腰三角形的周长为A．16B．18C．20D．16或202．下列说法中，错误的是A．平行四边形的对角线互相平分B．矩形的对角线互相垂直C．菱形的对角线互相垂直平分D．等腰梯形的对角线相等3.如图，梯形ABCD中，AD∥BC，AB=DC=3，AD=5，∠C=60°，则下底BC的长为A8B9C10D114.要判断小强同学的数学考试成绩是否稳定，那么需要知道他最近几次数学考试成绩的A．方差B．众数C．平均数D．中位数5.要使二次根式1x有意义，字母x必须满足的条件是A．x≥1B．x>－1C．x≥－1D．x>16.如图，四边形ABCD是矩形，AB:AD=4:3，把矩形沿直线AC折叠，点B落在点E处，连接DE，则DE:AC的值是A.1:3B.3:8C.8:27D.7:25二填空:(3分×10)7．等腰三角形一个角为700，则顶角的度数为.8．如图，在△ABC中，∠C=90°，∠A=30°，若AB=6cm，则BC=cm.9．如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=4,则点D到AB的距离为________.10．已知:□ABCD的周长是28㎝，△ABC的周长是22㎝，则AC的长为.11．如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是S1S2（填“＞”“＜”或“＝”）12．一组数据-1、2、3、6的极差.13．小明是学生会纪律检查委员，上周值日时他对我校迟到的学生进行了统计，统计结果如下表：星期星期一星期二星期三星期四星期五迟到人数24563则这组数据：2，4，5，6，3的标准差是.14．直接写出答案：_______)9(2，_______232.15.如图所示，每个小正方形边长为1，连接小正方形的三个顶点，可得△ABC，则△ABC的边AC上的高长度为.16．如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF=3，则小正方形的边长为.三解答题:(本大题共10小题,总分102分)17．(1)计算或化简：(3分×2)①156②914(2)(4分)长方形的面积为12cm2,一边长为10cm，求另一边长.18.(9分)若化简21816xxx的结果为25x，求x的取值范围.19.(5分×2)如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．（1）求证：△BEC≌△DFA；（2）求证：四边形AECF是平行四边形．20.(5分×2)如图，在四边形ABCD中，AB=BC，对角线BD平分ABC，P是BD上一点，过点P作PMAD，PNCD，垂足分别为M、N。(1)求证：ADB=CDB；(2)若ADC=90，求证：四边形MPND是正方形。21.(8分)如图所示，在梯形ABCD中，AD∥BC，AB=CD，E、F、G、H分别为边AB、BC、CD、DA的中点，求证：四边形EFGH为菱形．22.(5分×2)如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．（1）BD与CD有什么数量关系，并说明理由；（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．23.为了从甲．乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了如下统计图表：图1甲、乙射击成绩统计表平均数中位数方差命中10环的次数甲70乙1图2甲、乙射击成绩折线图（1）请补全上述图表（请直接在表中填空和补全折线图）；(6分)（2）如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；(3分)乙甲yx命中环数射击次数12345678910010987654321（3）如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？(2分)24.(5分×2)已知菱形ABCD的两条对角线分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上一点.（1）求菱形ABCD的面积.（2）求PM+PN的最小值.25.如图，在矩形ABCD中，AB=6,AD=2,点P在线段AB上运动，设AP=x，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原.（1）当0x时，折痕EF的长为；(2分)当点E与点A重合时，折痕EF的长为；(2分)（2）试探索使四边形EPFD为菱形时x的取值范围，并求当4x时,菱形EPFD的边长.(3分+3分)提示：用草稿纸折折看，或许对你有所帮助！F26.如图，在菱形ABCD中，AB=BD，点E，F分别在AB，AD上，且AE=DF．连接BF与DE相交于点G，连接CG与BD相交于点H．(6分+4分+4分)(1)求证:△AED≌△DFB；(2)求证:DEB=CBG；(3)求证:S四边形BCDG=CG2.