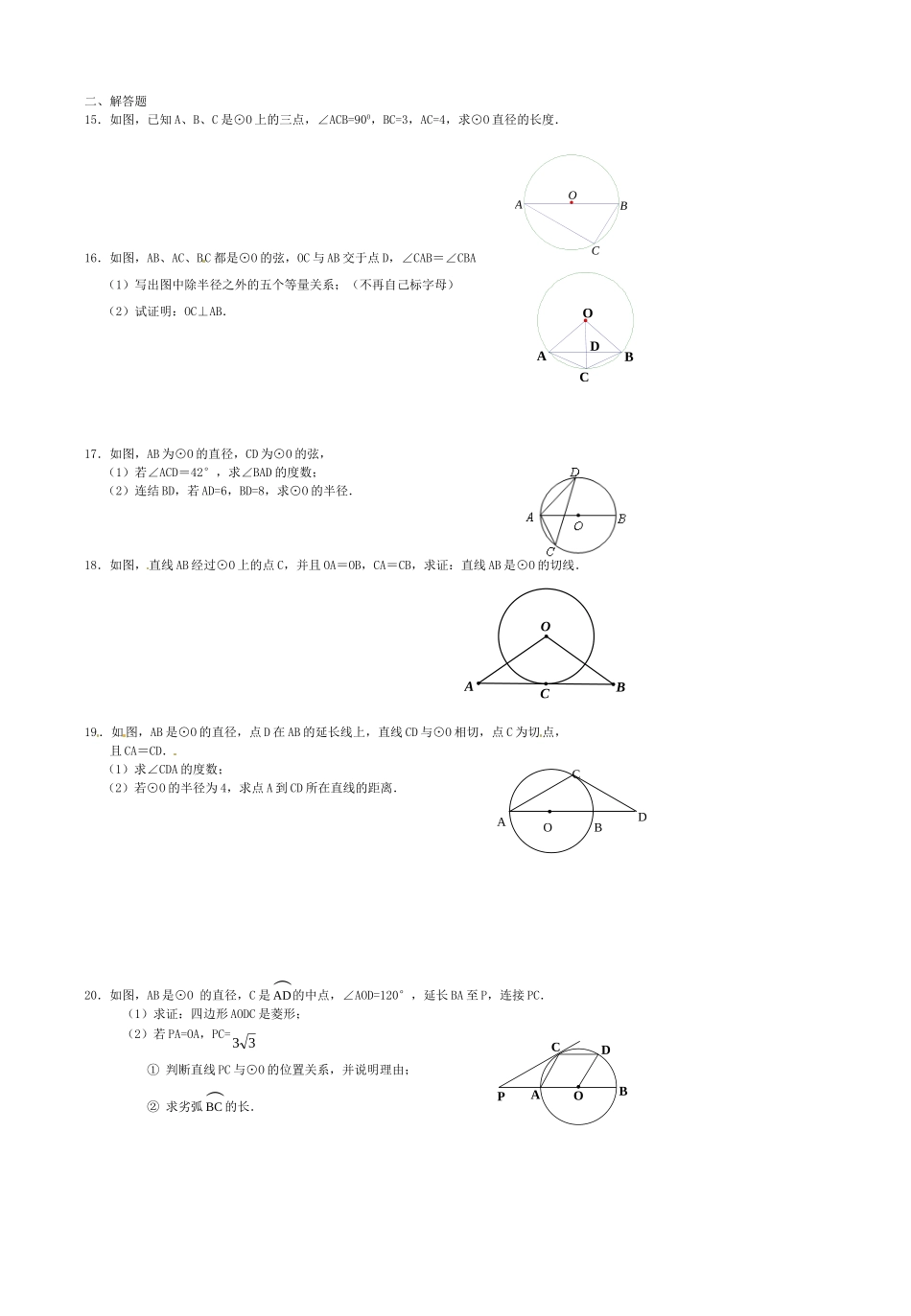
CABOEDCABOED图1ABCOABCOD图2图3ABOCDABCO图4ABCDO图5九年级上数学周末自测卷—圆3班级姓名座号一、选择题1.半径为cm2的正六边形的边心距等于()A.cm1B.cm3C.cm5D.cm22.已知⊙O的半径为cm6,弦AB所对的圆周角等于30,则弦AB的长为()A.cm3B.cm4C.cm5D.cm63.如图,⊙O的两条弦AE、BC相交于点D,连结AC、BE.若∠ACB=60°,则下列结论正确的是()A.∠AOB=60B.∠AEB=60C.∠ADB=60D.∠AEB=304.如图,AB是⊙O直径,CD是弦,AB与CD相交于点E,连结AC、AD、OD则下列结论不能成立的是()A.∠ACB=90B.∠ADC=∠ABCC.∠ACD=21∠AODD.∠DEB=21∠BOD5.Rt△ABC的两条直角边长分别为6、8,以直角顶点C为圆心,5为半径的⊙C与直线AB()A.相交B.相切C.相离D.相交或相切6.以半径为1的正三角形、正方形、正六边形的边心距为三边作三角形,则()A.不能构成三角形B.这个三角形是等腰三角形C.这个三角形是直角三角形D.这个三角形是钝角三角形7.如图2,在△ABC中,AB=AC=2,BC=2。以A为圆心作圆弧切BC于点D,且分别交边AB、AC于点E、F,则扇形AEF的面程是()A.8B.4C.2D.二、填空8.正三角形的中心角等于=°.9.(1)已知圆弧的半径为12,圆心角为60○,则此弧的弧长为.(2)一个扇形所在圆的半径为10,圆心角为108○,则扇形的面积为.(3)一个扇形所在圆的半径为6,扇形的面积为12,则扇形的圆心角为°.(4)已知扇形圆心角为150○,它所对弧长为20,则扇形半径是,扇形面积是.10.如图1,在⊙O中,△ABC的三个顶点都在圆周上,且∠OBC=40,则∠A=度.11.如图2,在⊙O中,AB是直径,∠AOC=130,则∠BDC=.12.如图3,在⊙O中,AB是直径,AC、CD是弦,AB=cm6,∠CDB=30,则∠ABC=,BC=,AC=.13.如图4,在⊙O中,弦AB等于它的半径,点C在优弧AB上,则∠ACB=.14.如图5,在⊙O中,AB是直径,点C.D在⊙O上,AC=BD,∠COD=40°,则∠COB=°,∠A=°.ABCDODOPCBABOCA二、解答题15.如图,已知A、B、C是⊙O上的三点,∠ACB=900,BC=3,AC=4,求⊙O直径的长度.16.如图,AB、AC、BC都是⊙O的弦,OC与AB交于点D,∠CAB=∠CBA(1)写出图中除半径之外的五个等量关系;(不再自己标字母)(2)试证明:OC⊥AB.17.如图,AB为⊙O的直径,CD为⊙O的弦,(1)若∠ACD=42°,求∠BAD的度数;(2)连结BD,若AD=6,BD=8,求⊙O的半径.18.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.19.如图,AB是⊙O的直径,点D在AB的延长线上,直线CD与⊙O相切,点C为切点,且CA=CD.(1)求∠CDA的度数;(2)若⊙O的半径为4,求点A到CD所在直线的距离.20.如图,AB是⊙O的直径,C是︵AD的中点,∠AOD=120°,延长BA至P,连接PC.(1)求证:四边形AODC是菱形;(2)若PA=OA,PC=33①判断直线PC与⊙O的位置关系,并说明理由;②求劣弧︵BC的长.OCBAOABDCOABCDECDAOBM21.如图,点A、B、C分别是⊙O上的点,∠B=600,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.(1)求证:AP是⊙O的切线;(2)求PD的长.22.如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与边BC相切于点M.(1)求证:CD与⊙O相切;(2)若⊙O的半径为1,求正方形ABCD的面积.23.如图,AB是⊙O的切线,B为切点,BC是⊙O的弦,直线AC与⊙O交于D,∠C=45°,DE⊥AB,垂足为E.(1)判断直线DE与⊙O的位置关系,并说明理由;(2)若∠A=30°,AB=232,求⊙O的半径.