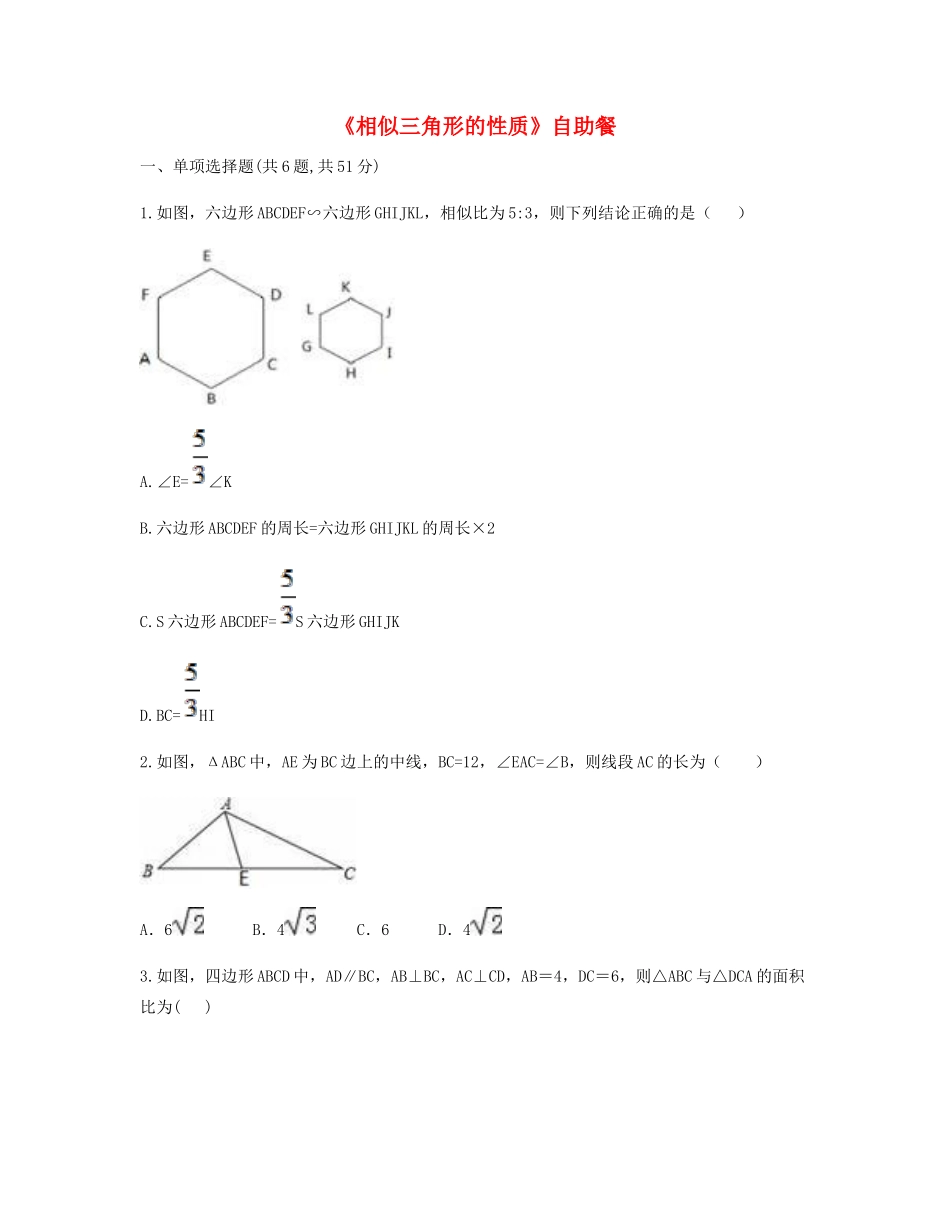
《相似三角形的性质》自助餐一、单项选择题(共6题,共51分)1.如图,六边形ABCDEF∽六边形GHIJKL,相似比为5:3,则下列结论正确的是()A.∠E=∠KB.六边形ABCDEF的周长=六边形GHIJKL的周长×2C.S六边形ABCDEF=S六边形GHIJKD.BC=HI2.如图,ΔABC中,AE为BC边上的中线,BC=12,∠EAC=∠B,则线段AC的长为()A.6B.4C.6D.43.如图,四边形ABCD中,AD∥BC,AB⊥BC,AC⊥CD,AB=4,DC=6,则△ABC与△DCA的面积比为()A.2∶3B.4∶9C.2∶5D.∶4.如图,已知菱形ABCD的面积为50,把菱形ABCD沿着对角线AC向右平移得到菱形EFGH.当AE=AC时,则图中阴影部分的面积为()A.50B.60C.64D.805.如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面直径为1.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为()A.0.64米2B.0.81米2C.1.44米2D.5.76米26.如图,矩形ABCD中,AD=15,AB=10,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()A.B.C.D.二、填空题(共3题,共25分)1.如图,△ABC中,AB=15,AC=12,BC=18.如果动点D以每秒3个单位长度的速度从点B出发沿边BA向点A运动,此时直线DE∥BC,交AC于点E.记x秒时DE的长度为y,则y关于x的函数关系是____________________.(要写出x的取值范围)2.已知:在平行四边形ABCD中,点E在直线AD上,AE=AD,连接CE交BD于点F,则EF:FC的值是.3.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=,则BD的长为_______.三、解答题(共3题,共24分)1.如图,P是矩形ABCD边BC上一点,∠APF=90°,PF交AC于M,交CD于F,BN⊥AC于N,BN交AP于点H.(1)求证:△ABP∽△PCF;(2)找出图中与△ABH相似的三角形,并证明;(3)若P是BC中点,BC=2AB,AB=2,求PM的长.2.如图,在Rt△ABC中,∠ACB=90°,BC=cm,∠ABC=30°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒cm的速度向点B匀速运动,设运动时间为t秒(0),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值;(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.3.如图,在Rt△ABC中,斜边BC=cm,AB=2cm,点P,Q同时以1cm/秒的速度分别从点A,B出发,在线段AB上相向而行.当点P到达点B时,P,Q两点同时停止运动.以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为t秒,正方形APDE和梯形BCFQ重合部分的面积为Scm2.(1)当t=_____秒时,点P与点Q重合;(2)当t=_____秒时,点D在QF上;(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.