内蒙古阿拉善右旗 八年级数学上学期期中试题(无答案) 试题VIP免费

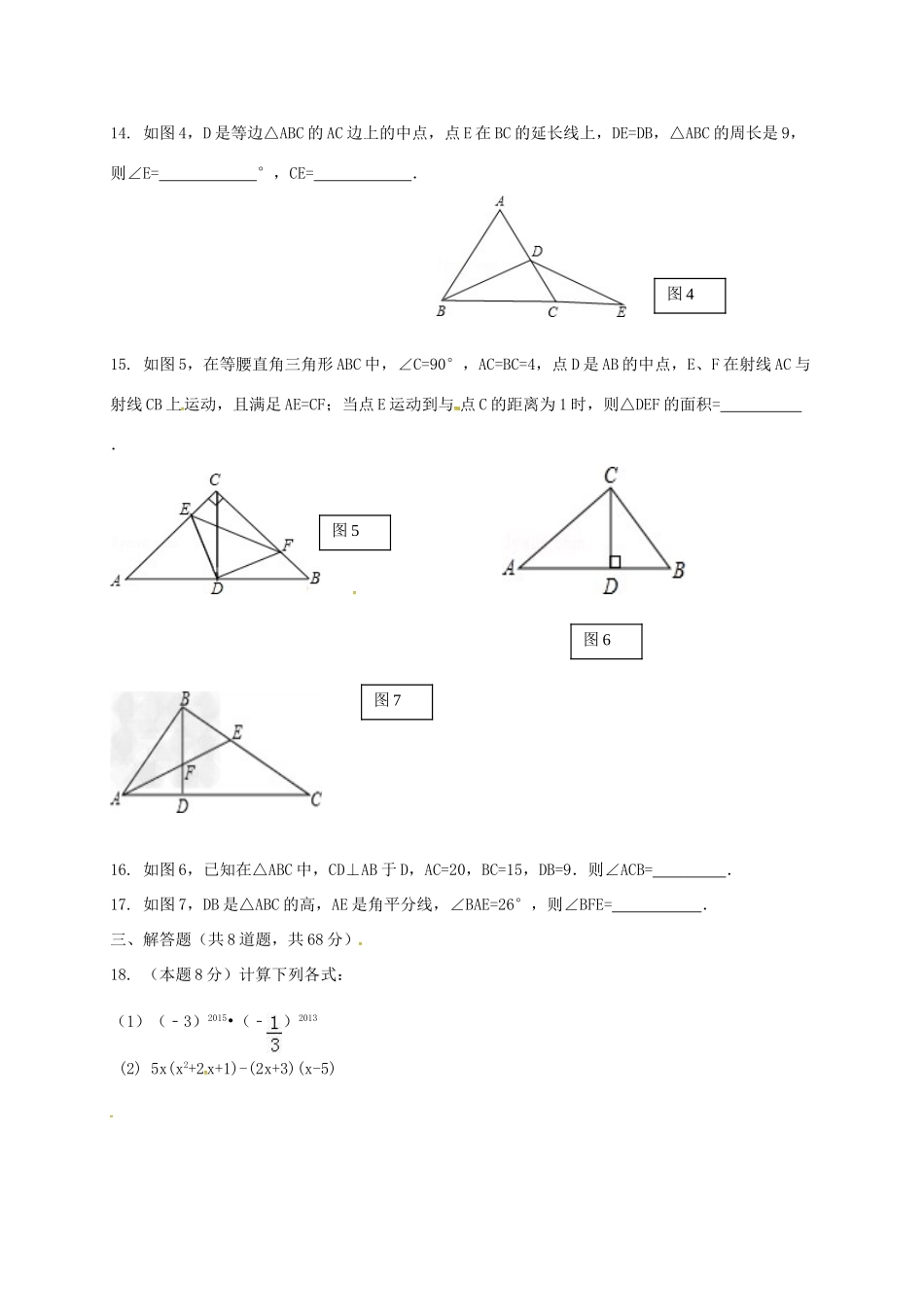
内蒙古阿拉善右旗2016-2017学年八年级数学上学期期中试题一、选择题（共12小题，每小题3分，满分36分）1.下列四个图案中，是轴对称图形的是（）2.点M（3，－4）关于x轴的对称点的坐标是（）A.（3，4）B.（－3，－4）C.（－3，4）D.（－4，3）3.下列计算正确的是（）A．a3+a2=a5B.（3a﹣b）2=9a2﹣b2C.a6b÷a2=a3bD.（﹣ab3）2=a2b64.如图1，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，△ABC的面积为7，DE=2，AB=4，则AC长是（）A．2B．3C．4D．55.如图2，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（）A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=90°6.下列说法中，错误的是（）A．任意两条相交直线都组成一个轴对称图形B．等腰三角形最少有1条对称轴，最多有3条对称轴C．成轴对称的两个三角形一定全等D．全等的两个三角形一定成轴对称7.一个三角形的三个外角之比为3：3：2，则这个三角形是（）A．等腰三角形B．等腰直角三角形C．直角三角形D．等边三角形8.和三角形三条边距离相等的点是（）A．三条角平分线的交点B．三边中线的交点图1图2C．三边上高所在直线的交点D．三边的垂直平分线的交点9.如图，AD是△ABC的角平分线,从点D向AB、AC两边作垂线段，垂足分别为E、F，那么下列结论中错误的是（）A．DE=DFB．AE=AFC．BD=CDD．∠ADE=∠ADF10.如图，△ABC中，∠C＝90°，∠A＝30°，AB的垂直平分线交AC于D，交AB于E，CD＝2，则AC等于（）A．4B.5C.6D.811.如果三角形一条边上的中线等于这条边的一半，那么这个三角形是（）A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形12.如图3，三角形ABC中，∠A的平分线交BC于点D，过点D作DE⊥AC，DF⊥AB，垂足分别为E，F，下面四个结论：①∠AFE=∠AEF；②AD垂直平分EF；③；④EF一定平行BC．其中正确的是（）A．①②③B．②③④C．①③④D．①②③④题号123456789101112答案二、填空题(共5道题，每题3分，14题4分，共16分)13.等腰三角形的周长为14，其一边长为4，那么它的底边长为．（第9题）CFEADBDEACB10题图314.如图4，D是等边△ABC的AC边上的中点，点E在BC的延长线上，DE=DB，△ABC的周长是9，则∠E=°，CE=．15.如图5，在等腰直角三角形ABC中，∠C=90°，AC=BC=4，点D是AB的中点，E、F在射线AC与射线CB上运动，且满足AE=CF；当点E运动到与点C的距离为1时，则△DEF的面积=．16.如图6，已知在△ABC中，CD⊥AB于D，AC=20，BC=15，DB=9．则∠ACB=．17.如图7，DB是△ABC的高，AE是角平分线，∠BAE=26°，则∠BFE=．三、解答题（共8道题，共68分）18.（本题8分）计算下列各式：（1）（﹣3）2015•（﹣）2013(2)5x(x2+2x+1)-(2x+3)(x-5)图4图5图6图719.（本题8分）如图，在△ABC中，AB=AC=6，BC=10，AB的垂直平分线分别交BC、AB于点D、E.（1）求△ACD的周长；（2）若∠C=25°，求∠CAD的度数.20.（本题8分）如图，△ABC中，AB=AC=5，AB的垂直平分线DE交AB、AC于E、D．①若△BCD的周长为8，求BC的长；②若BD平分∠ABC，求∠BDC的度数．21.（本题8分）已知，如图所示，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．22.（本题8分）如图，ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于DCBEA图8ABCDEE、F，求证:EF=BE+CF.23.（本题10分）如图8，在ABC中，090ACB，CEBEBCAC,于E，ADCE于D.（1）求证：△ADC≌△CEB.（2）,5cmADcmDE3，求BE的长度.24.（本题8分）作图一：如图1，方格纸中每个小正方形的边长均为1，四边形ABCD的四个顶点都在小正方形的顶点上，点E在BC边上，且点E在小正方形的顶点上，连接AE．第22题（1）在图中画出△AEF，使△AEF与△AEB关于直线AE对称，点F与点B是对称点；（2）请直接写出△AEF与四边形ABCD重叠部分的面积．作图二：如图2，△ABC与△DEF关于直线l对称，请仅用无刻度的直尺，在图2中作出直线l．（保留作图痕迹）25.（本题10分）如图在△ABC中，D是BC的中点，过点D的直线GF交AC于点F，交AC的平行线BG于点G，DE⊥GF，交AB于点E，连接EG，EF．求证：（1）EG=EF；(2)请你判断BE+CF与EF的大小关系，并证明你的结论.