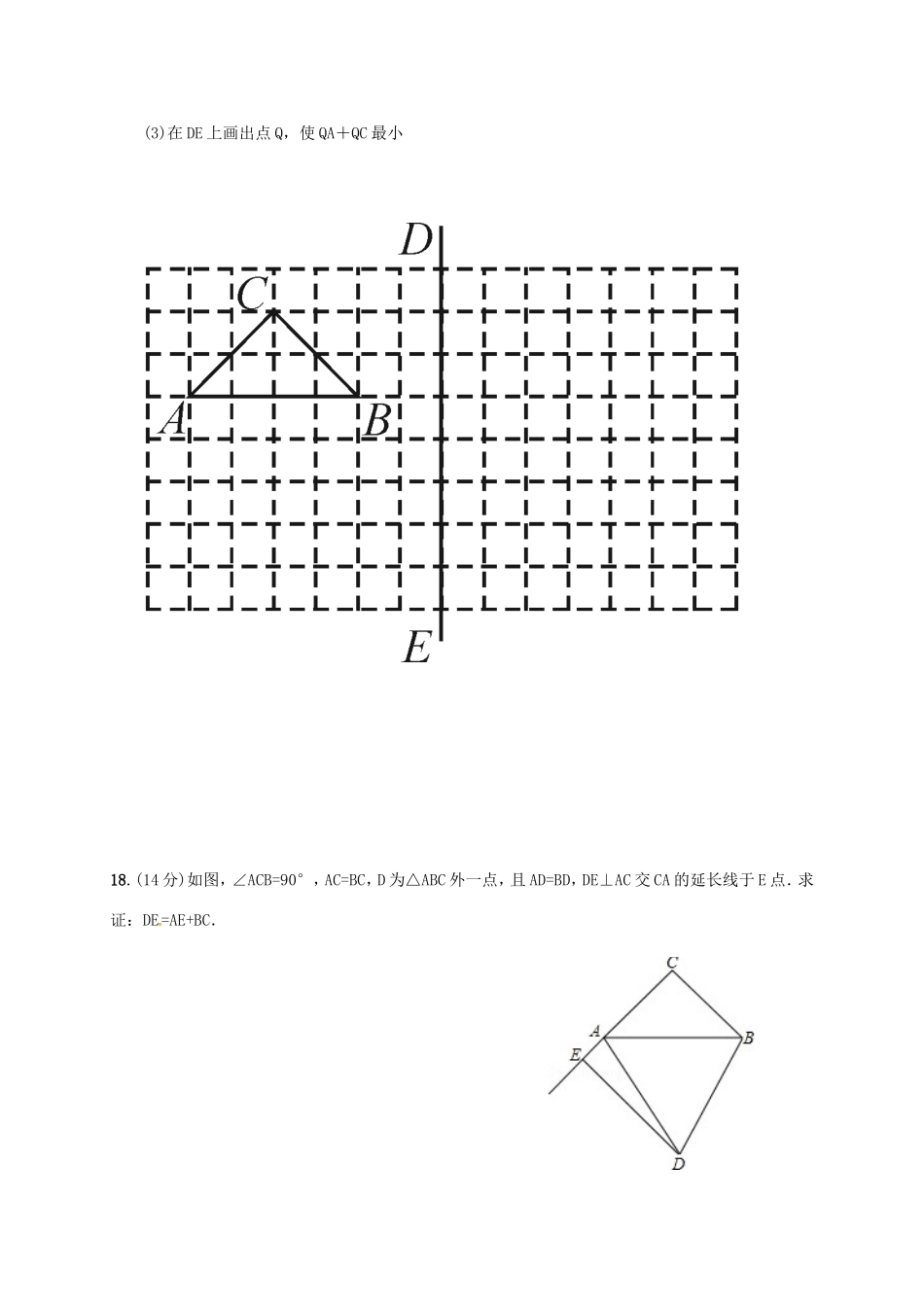
第十三章轴对称单元补偿题班级________姓名________考号________一、选择题(每题4分,共40分)1.下列图标中,是轴对称图形的是()(第1题)A.(1)(4)B.(2)(4)C.(2)(3)D.(1)(2)2.下列图形对称轴最多的是()A.正方形B.等边三角形C.等腰三角形D.线段3.和点P(-3,2)关于y轴对称的点是()A.(3,2)B.(-3,2)C.(3,-2)D.(-3,-2)4.如图,直线m是多边形ABCDE的对称轴,其中∠A=120°,∠B=110°,那么∠BCD的度数为()A.50°B.60°C.70°D.80°5.在平面直角坐标系xOy中,已知点A(2,-2),在y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有()A.1个B.2个C.3个D.4个6.已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则以点P1,O,P2为顶点的三角形是()A.直角三角形B.钝角三角形C.等腰三角形D.等边三角形(第4题)(第7题)(第8题)(第9题)7.如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为()A.48°B.36°C.30°D.24°8.如图,先将正方形纸片对折然后展开,折痕为MN,再把点B折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的是()A.AH=DH≠ADB.AH=DH=ADC.AH=AD≠DHD.AH≠DH≠AD9.如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是()A.40°B.30°C.20°D.10°10.△ABC是等腰三角形(AB=AC≠BC),在△ABC所在平面内有一点P,且使得△ABP,△ACP,△BCP均为等腰三角形,则符合条件的点P共有()A.1个B.4个C.5个D.6个二、填空题(每题4分,共24分)11.已知P1点关于x轴的对称点P2(3-2a,2a-5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是_____________.12.已知等腰三角形的一个内角是80°,则它的底角是_____________.13.如图,在△ABC中,若BC=6cm,AC=4cm,AB边的垂直平分线交AB于点E,交BC于点D,则△ADC的周长是________.(第13题)(第14题)(第15题)14.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=________.15.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形有________个.16.已知C,D两点在线段AB的垂直平分线上,且∠ACB=40°,∠ADB=68°,则∠CAD=_____________.三、解答题(共56分)17.(12分)如图,在所给网格图(每小格边长均是1的正方形)中完成下列各题:(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)在DE上画出点P,使PB1+PC最小;(3)在DE上画出点Q,使QA+QC最小18.(14分)如图,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E点.求证:DE=AE+BC.19.(14分)如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,FG⊥BC于G,请猜测AE与FG之间有怎样的数量关系,并说明理由..20.(16分)如图,在△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,延长DF交AB于点E,连接CE.(1)求证:AE=CE=BE;(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小?并求出此时PB+PC的值.