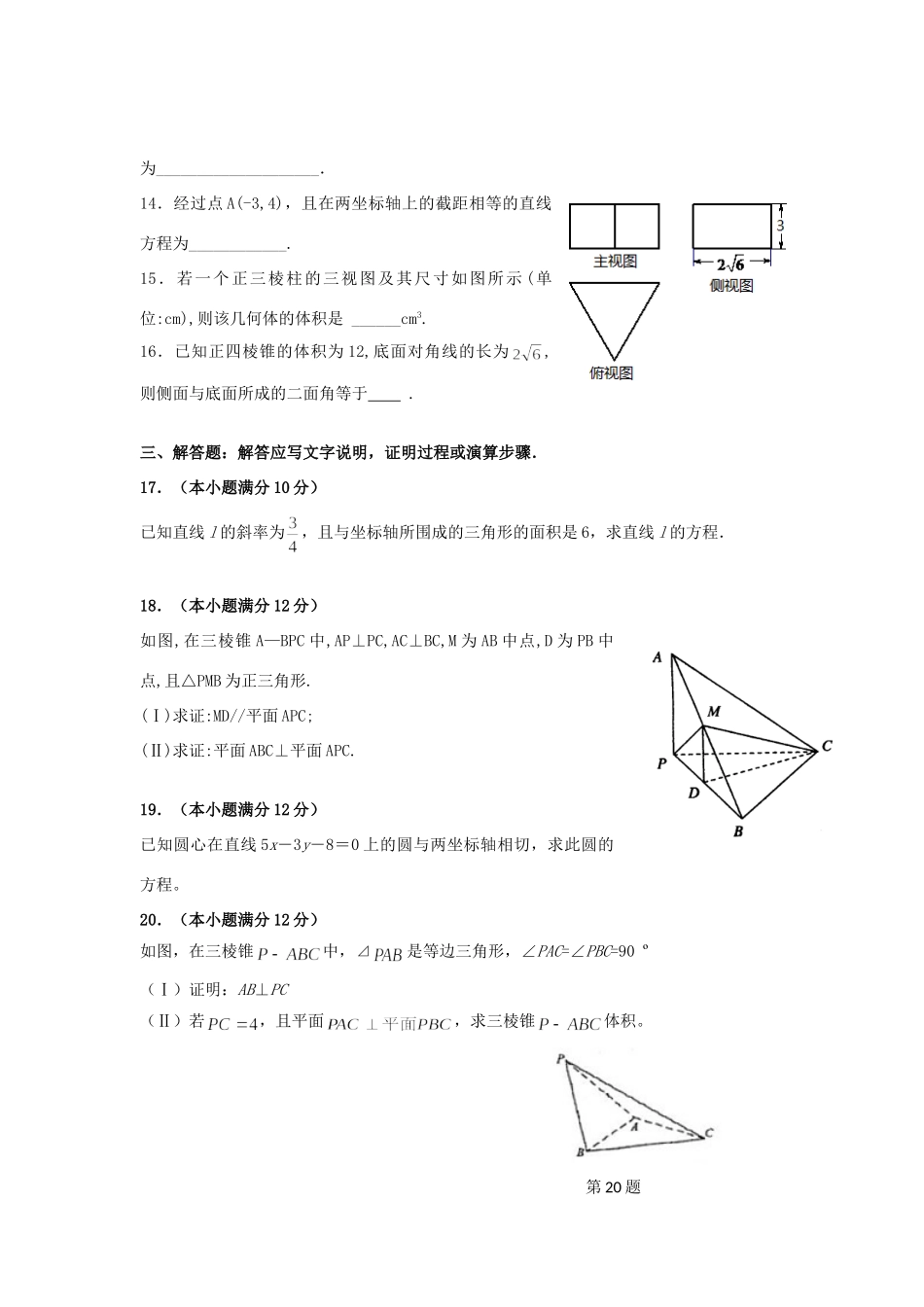
屯留一中2012-2013学年第一学期期中考试高二数学试题(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若直线的倾斜角为1200,则直线的斜率为:()A.B.C.D.2.右面三视图所表示的几何体是().A.三棱锥B.四棱锥C.五棱锥D.六棱锥3.平行线和的距离是()A.B.2C.D.4.在下列关于直线与平面的命题中真命题是()(A)若且,则(B)若且,则(C)若且,则(D)若且,则5.点在平面上的射影为,且==,那么是的()A.垂心B.外心C.内心D.重心6.与圆同圆心,且面积为圆C面积的一半的圆的方程为()A.B.C.D.7.在同一直角坐标系中,表示直线与正确的是()左视图正视图俯视图xyOxyOxyOxyOA.B.C.D.8.直线mx-y+2m+1=0经过一定点,则该点的坐标是()A.(-2,1)B.(2,1)C.(1,-2)D.(1,2)9.已知两定点,,如果动点P满足,则点P的轨迹所包围的面积等于()A.B.C.D.10.若使得方程有实数解,则实数m的取值范围为()11.正六棱锥底面边长为a,体积为a3,则侧棱与底面所成的角为().A.30°B.45°C.60°D.75°12.设为两两不重合的平面,为两两不重合的直线,给出下列四个命题:①若,,则;②若,,,,则;③若,,则;④若,,,,则。其中真命题的个数是()A.1B.2C.3D.4二、填空题:本大题共4小题,每小题5分.13.若直线3x-4y+12=0与两坐标轴的交点为A,B,则以线段AB为直径的圆的一般方程为____________________.14.经过点A(-3,4),且在两坐标轴上的截距相等的直线方程为____________.15.若一个正三棱柱的三视图及其尺寸如图所示(单位:cm),则该几何体的体积是______cm3.16.已知正四棱锥的体积为12,底面对角线的长为,则侧面与底面所成的二面角等于.三、解答题:解答应写文字说明,证明过程或演算步骤.17.(本小题满分10分)已知直线l的斜率为,且与坐标轴所围成的三角形的面积是6,求直线l的方程.18.(本小题满分12分)如图,在三棱锥A—BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.(Ⅰ)求证:MD//平面APC;(Ⅱ)求证:平面ABC⊥平面APC.19.(本小题满分12分)已知圆心在直线5x―3y―8=0上的圆与两坐标轴相切,求此圆的方程。20.(本小题满分12分)如图,在三棱锥中,⊿是等边三角形,∠PAC=∠PBC=90º(Ⅰ)证明:AB⊥PC(Ⅱ)若,且平面,求三棱锥体积。第20题21.(本小题满分12分)已知半径为5的圆C的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y-29=0相切.(1)求圆C的方程;(2)设直线ax-y+5=0与圆C相交于A,B两点,求实数a的取值范围;22.(本小题满分12分)如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为.(1)求侧面PAD与底面ABCD所成的二面角的大小;(2)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.(第22题)DBACOEP