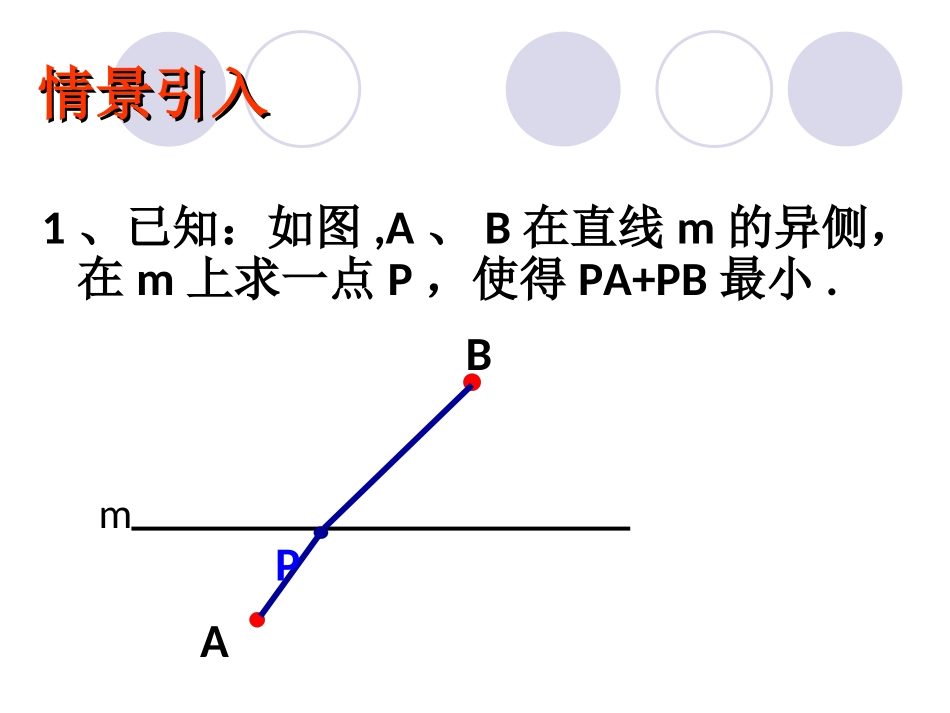
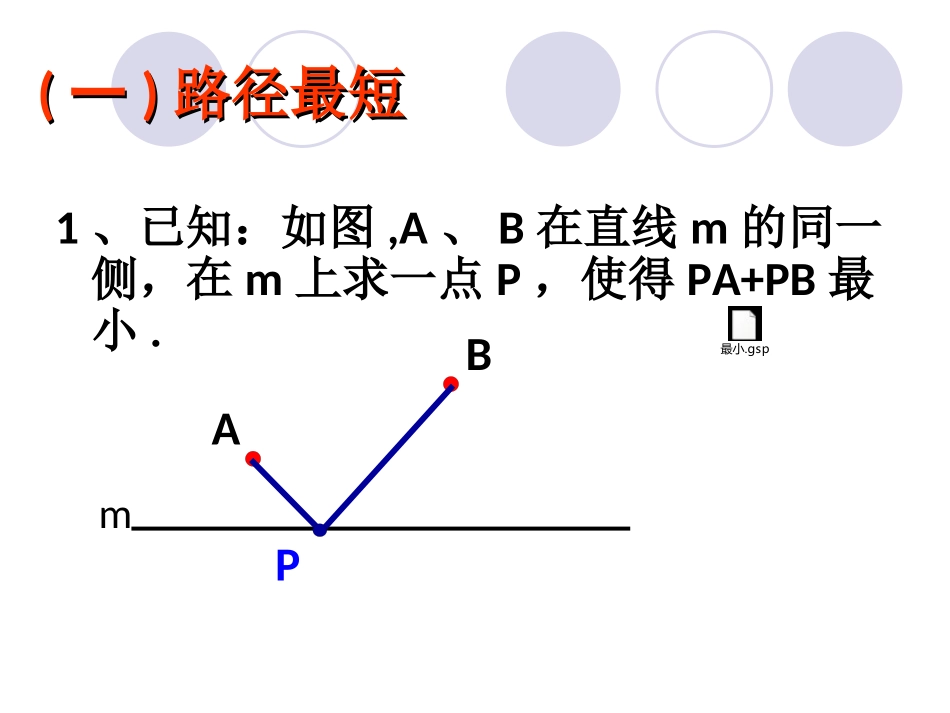
第十三章轴对称13.4课题学习路径之“最”问题1、已知:如图,A、B在直线m的异侧,在m上求一点P,使得PA+PB最小.情景引入情景引入ABmP1、已知:如图,A、B在直线m的同一侧,在m上求一点P,使得PA+PB最小.PABm最小.gsp((一一))路径最短路径最短ABmB′P点P即为所求.M作法:①作点B关于直线m的对称点B′.②连接AB′,交直线m于点P.为什么这样做最短距离呢?MA+MB=MA+MB′>AB′即MA+MB′>PA+PB三角形任意两边之和大于第三边解决问题解决问题解题策略:设法把若干线段转化到同一条线段上.比如作已知点的对称点,连接对称点与另一已知点(或连接两个对称点).理论依据:三角形两边之和大于第三边;两边之差小于第三边(两点之间,线段最短).归纳总结:CDFM最短路线:CMNDBA变化一如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。NEO变化应用变化应用证明:在OA上任取一点G,OB上任取一点H,连接CG、GH、DH…∵点F,点C关于直线OA对称,点G.M在OA上,∴GF=GC,FM=CM,同理HD=HE,ND=NE,∴CM+MN+ND=FM+MN+NE=FE,CG+GH+HD=FG+GH+HE,在四边形EFGH中,∵FG+GH+HE>FE,即CG+GH+HD>CM+MN+ND∴CM+MN+ND最短FAOBD··CEMNGH变化二已知:如图锐角∠MON内部任意一点A,在∠MON的两边OM,ON上各取一点B,C,组成三角形ABC,使三角形周长最小.分析:当AB、BC和AC三条边的长度恰好能够转化到一条线段上时,三角形的周长最小MNAA′A″BC((二二))路径最长问题路径最长问题1.(根据黄冈中考题改编)已知直角坐标系中两点A(1,3),B(2,1)和X轴上一动点P,当PA与PB的差最大时,求点P的坐标.变化如图,已知直线m两侧点A、B,直线m上一动点P,若PA-PB最大,请作出P点。APBB′P′分析:我们可以把点B转化到直线m的另一侧,与点A同侧。m总结本节课我们学习了路径最长(或最短)问题,这类问题的解决方法主要是:设法把若干条线段转化到同一条线段上.