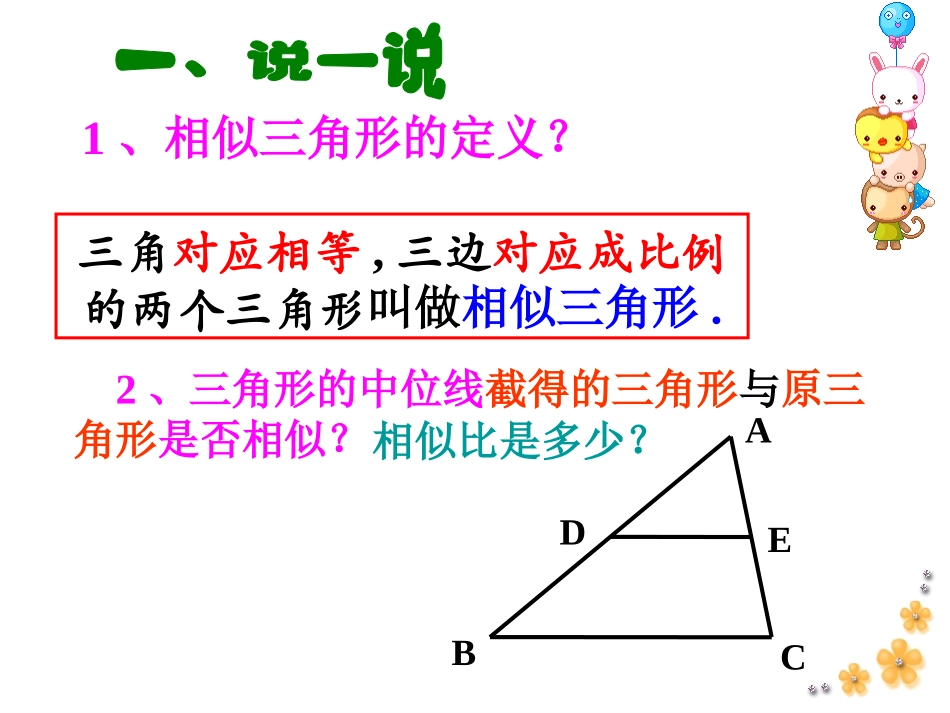
2、三角形的中位线截得的三角形与原三角形是否相似?相似比是多少?1、相似三角形的定义?ABCDE三角对应相等,三边对应成比例的两个三角形叫做相似三角形.•如图在△ABC中,点D,E分别在AB,AC上,且DE‖BC,则△ADE与△ABC相似吗?•(1)议一议:这两个三角形的三个内角是否对应相等?•(2)量一量这两个三角形的边长,它们是否对应成比例?平行移动DE的位置再试一试.合作学习:ABCDE平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.ABCDEFIJGH分析:要证两个三角形相似,目前只有两个途径。一个是三角形相似的定义,(显然条件不具备);二是利用平行线来判定三角形相似的定理。为了使用它,就必须创造具备定理的基本图形的条件。怎样创造呢?ABCA’C’B’命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。已知:在△ABC和△A’B’C’中,A=A’,B=B’,∠∠∠∠求证:ΔABCA’B’C’∽△(把小的三角形移动到大的三角形上)。怎样实现移动呢?在△ABC边AB上,截取AD=A’B’,过D作DEBC∥交AC于E.则有△ADEABC∽△∴△A'B'C'ABC.∽△证明:CBADEA’B’C’∵∠ADE=B,B=B'∠∠∠∴∠ADE=B'∠又∵∠A=A',AD=A'∠B'∴△ADEA'B'C'(ASA)△在△ABC边AB上,截取AD=A’B’,在AC边上截取AE=A’C’.则有△ADE≌△A'B'C'∴△A'B'C'ABC∽△证明:CBADEA’B’C’∴∠ADE=B'∠=B∠∴DEBC∥△ADEABC∽△∴判定定理判定定理11::如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。练习:已知:ΔABC和ΔDEF中,∠A=400,∠B=800,∠E=800,∠F=600。求证:ΔABCΔDEF∽AFECBD400800800600606000(1)、已知ΔABC与ΔA/B/C/中,∠B=B∠/=750,∠C=500,∠A/=550,这两个三角形相似吗?为什么?ABCA/B/C/750750500550550(2)已知等腰三角形ΔABC和ΔA/B/C/中,∠A、∠A/分别是顶角,求证:①如果∠A=A∠/,那么ΔABCΔA∽/B/C/。②如果∠B=B∠/,那么ΔABCΔA∽/B/C/。ABCA/B/C/ABCA/B/C/•例1、在一次数学活动课上,为了测量河宽AB,小张采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)BACDE例2在一次数学活动课上,为了测量河宽AB,张杰采用了如下的方法(如图)从A处沿与AB垂直的直线方向走40米到达C处,插一根标竿,然后沿同方向继续走15米到达D处,再向右转90度走到E处,使B、C、E三点恰好在一条直线上,量得DE=20米,这样就可以求出河宽AB,请你算出结果(要求写出解题过程)。ABDCEABDEO方法二方法三方法一CDF练习求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。ADBC已知:在RtΔABC中,CD是斜边AB上的高。求证:ΔABCΔACD∽ΔCBD。∽证明:∵∠B=B∠,∠CDB=ACB=90°∠,∴△ABCCDB∽△(两个角对应相等,两三角形相似).同理可证:△ABCACD∽△△ABCCBDACD.∽△∽△此结论可以称为“母子相似定理母子相似定理”,今后可以直接使用.ABCE延伸练习已知:如图,在ΔABC中,AD、BE分别是BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出。D(1)求证:ΔAEFΔADC∽;FAFEDCΔAEFΔADCΔBECΔBDF.∽∽∽1.过Rt△ABC的斜边AB上一点D作一条直线与另一边AC或者BC相交,使截得的小三角形与△ABC相似,这样的直线有几条?ACD●AB课外思考题:如图,在ΔABC中,点D、E分别是边AB、AC上的点,连结DE,利用所学的知识讨论:当具备怎样的条件时,ΔADE与ΔABC相似?ABCDEABCDE(提示:有两种可能)(提示:有两种可能)课堂小结。作业。1、课后作业题2、作业本3、全效学习。1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.2、相似三角形的判定定理1:两角对应相等,两两角对应相等,两三角形相似。三角形相似。3、母子相似定理:直角三角形被斜边上的高分成的两个直直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。角三角形和原三角形相似。4.相似三角形判定定理的应用.4.相似三角形判定定理的应用.