1.5.3定积分的概念 (2)VIP免费

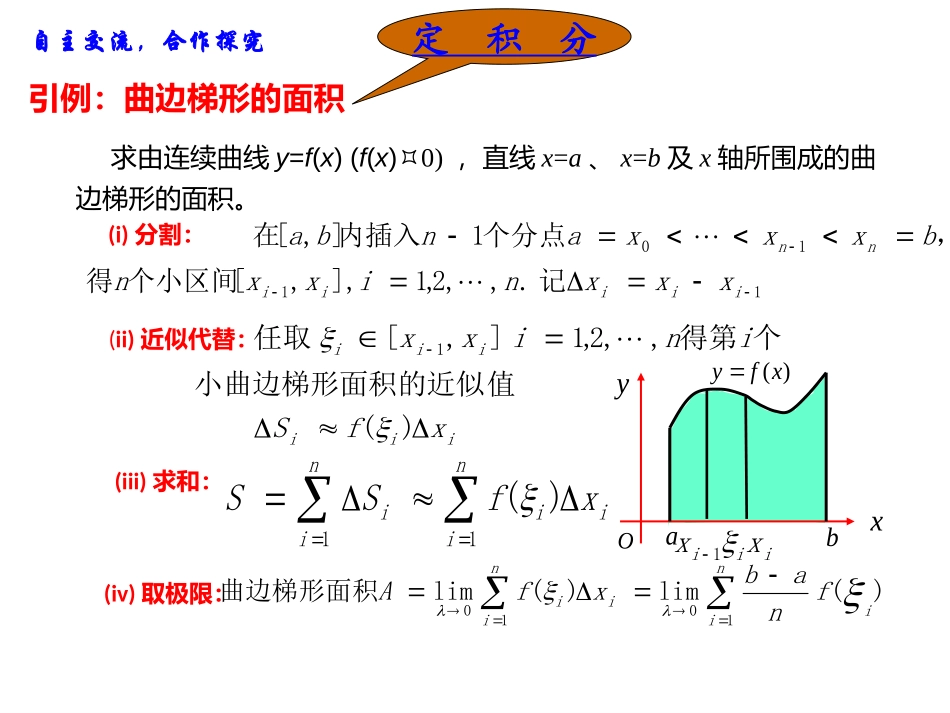
1.5.3定积分的概念承德市双滦区实验中学冯迪从求曲边梯形面积以及变速直线运动路程的过程可知，它们都可以通过“四步曲”：分割、近似代替、求和、取极限得到解决，且都可以归结为求一个特定形式和的极限.求由连续曲线y=f(x)(f(x)0)，直线x=a、x=b及x轴所围成的曲边梯形的面积。引例：曲边梯形的面积1110记.,,2,1],,[个小区间得，个分点1内插入],[在iiiiinnxxxnixxnbxxxanba(i)分割：iiiiiixfSinixx)(值小曲边梯形面积的近似个得第,,2,1],[任取1(ii)近似代替：niiiniixfSS11)((iii)求和：(iv)取极限：)(lim)(lim曲边梯形面积1010niiiinifnabxfAOabxy)(xfyiiixx1定积分自主交流，合作探究一、定积分的概念bxxxxxabaxfnii110上连续，用分点]，[）在区间（一般地，如果函数，）（）（），作和式，，2，1（上任取一点]，[间个小区间，在每个小区等分成]，[将区间111niniiiiiifnabxfnixxnba.][上的定积分，）在区间（叫做函数某个常数，这个常数时，上述和式无限接近当baxfn.lim1niinbabafnabdxxfdxxf）（）（，即）（记作归纳总结形成概念定积分的定义：定积分的相关名称：———叫做积分号，f(x)——叫做被积函数，f(x)dx—叫做被积表达式，x———叫做积分变量，a———叫做积分下限，b———叫做积分上限，[a,b]—叫做积分区间。1()lim()ninibafxdxfnba即Oabxy)(xfySbaf(x)dx；按定积分的定义，有(1)由连续曲线y=f(x)(f(x)0)，直线x=a、x=b及x轴所围成的曲边梯形的面积为(2)设物体运动的速度v=v(t)，则此物体在时间区间[a,b]内运动的距离s为sbav(t)dt。Oab()vvttv定积分的定义：1()lim()ninibafxdxfnba即112001()3Sfxdxxdx根据定积分的定义右边图形的面积为1xyOf(x)=x213S2()2vtt=-+Ovt12112005()(2)3Svtdttdt根据定积分的定义左边图形的面积为1.()bafxdx是一个和式的极限，是一个确定的常数2.当xfini)(1的极限存在时，其极限值仅与被积函数及积分区间有关，而与区间ba,的分法及i点的取法无关。f(x)[a,b]3．定积分的值与积分变量用什么字母表示无关，即有bababaduufdttfdxxf)()()(说明Oxyabyf(x)baf(x)dxcaf(x)dxbcf(x)dx。x=a、x=b与x轴所围成的曲边梯形的面积。当f(x)0时，积分dxxfba)(在几何上表示由y=f(x)、特别地，当ab时，有baf(x)dx0。定积分的几何意义：问题探究当f(x)0时，由yf(x)、xa、xb与x轴所围成的曲边梯形位于x轴的下方，xyOdxxfSba)]([=-，dxxfba)(．abyf(x)y-f(x)dxxfSba)]([baf(x)dxcaf(x)dxbcf(x)dx。=-S上述曲边梯形面积的负值。积分baf(x)dx在几何上表示baf(x)dxcaf(x)dxbcf(x)dx。=-S,0)(xfbaAdxxf)(曲边梯形的面积,0)(xfbaAdxxf)(曲边梯形的面积的相反数也就是：y)(xfyaxbxxoAy)(xfyaxbxAxo特别地，当ab时，有baf(x)dx0。oabxyy=f１(x)ＢＡy=f２(x)ＤＣ根据定积分的几何意义，你能用定积分表示图中阴影部分的面积吗？12()()bbaaSfxdxfxdx问题探究定积分的基本性质性质1.dx)]x(g)x(f[bababadx)x(gdx)x(f性质2.badx)x(kfbadx)x(fk定积分关于积分区间具有可加性bccabadxxfdxxfdxxf)()()(性质3.2121ccbccabadx)x(fdx)x(fdx)x(fdx)x(fOxyabyf(x)Ｃ3fxx解：令在区间[0,1]上等间隔地插入n-1个分点，把区间[0,1]等分成n个小区间每个小区间的长度为i-1i,i=1,2,,nin（）ii-11Δx=-=nnn(1)分割例题分析的值。x计算、利用定积分的定义，1例103dx（2）近似代替，作和1n3nnn133n40i=1i=1i=12224ii1xdxS=fx==innn1111=nn+1=1+n44n213n0nn111xdx=limS=lim1+=4n4（3）取极限iiξ=(i=1,2,,n)n取，例2、...