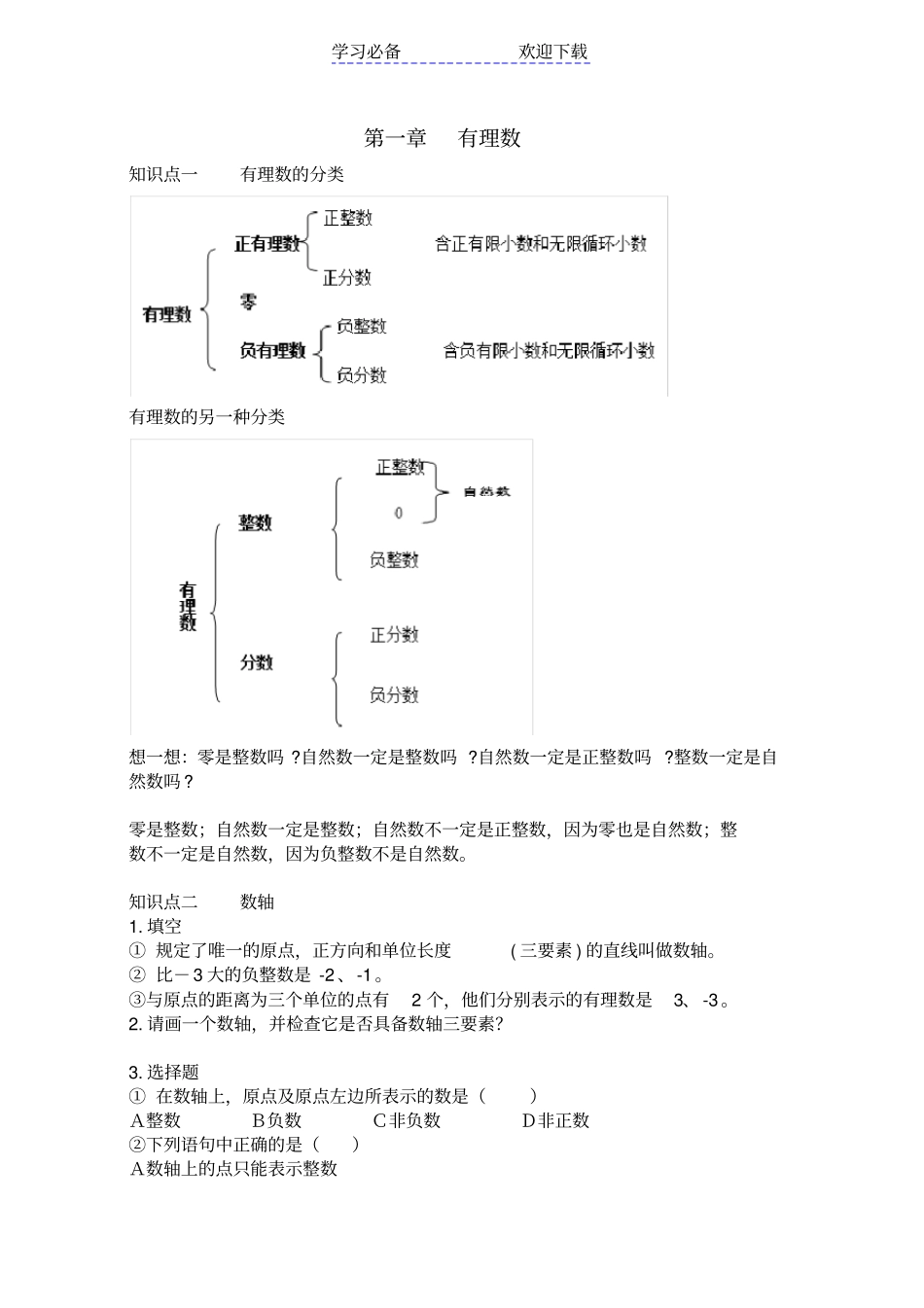
学习必备欢迎下载第一章有理数知识点一有理数的分类有理数的另一种分类想一想:零是整数吗?自然数一定是整数吗?自然数一定是正整数吗?整数一定是自然数吗?零是整数;自然数一定是整数;自然数不一定是正整数,因为零也是自然数;整数不一定是自然数,因为负整数不是自然数。知识点二数轴1.填空①规定了唯一的原点,正方向和单位长度(三要素)的直线叫做数轴。②比-3大的负整数是-2、-1。③与原点的距离为三个单位的点有2个,他们分别表示的有理数是3、-3。2.请画一个数轴,并检查它是否具备数轴三要素?3.选择题①在数轴上,原点及原点左边所表示的数是()A整数B负数C非负数D非正数②下列语句中正确的是()A数轴上的点只能表示整数学习必备欢迎下载B数轴上的点只能表示分数C数轴上的点只能表示有理数D所有有理数都可以用数轴上的点表示出来答案AD知识点三相反数相反数:只有符号不同的两个数互为相反数,0的相反数是0。在数轴上位于原点两侧且离原点距离相等。知识点四绝对值1.绝对值的几何意义:一个数所对应的点离原点的距离叫做该数的绝对值。2.绝对值的代数定义:(1)一个正数的绝对值是它本身;(2)一个负数数的绝对值是它的相反数;(3)0的绝对值是0;(4)|a|大于或者等于0。3.比较两个数的大小关系数学中规定:在数轴上表示有理数,它们从左到右的顺序,就是从大到小的顺序,即左边的数小于右边的数。由此可知:(1)正数大于0,0大于负数,正数大于负数;(2)两个负数,绝对值大的反而小。知识点五有理数加减法1.同号两数相加,取相同的符号,并把绝对值相加。绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。2.互为相反数的两个数相加得0。3.一个数同0相加,仍得这个数。4.减去一个数,等于加上这个数的相反数。知识点六乘除法法则1.两数相乘,同号得正,异号得负,并把绝对值相乘。0乘以任何数,都得0。2.几个不为0的数相乘,积的符号由负因数的个数确定,负因数的个数为偶数时,积为正;负因数的个数为奇数时,积为负。3.两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0。4.有理数中仍然有:乘积是1的两个数互为倒数。5.除以一个不等于0的数等于乘以这个数的倒数。知识点七乘方乘方定义:求n个相同因数的积的运算,叫做乘方。负数的奇次幂是负数,负数的偶次幂是正数。正数的任何次幂都是正数,0的学习必备欢迎下载任何正整数次幂都是0。知识点八运算律及混合运算1.加法交换律:a+b=b+a1.加法交换律:a+b=b+a2.乘法交换律:a·b=b·a3.加法结合律:a+(b+c)=(a+b)+c4.乘法结合律:a·(b·c)=(a·b)·c5.乘法分配律:a·(b+c)=ab+ac6.有理数混合运算顺序:先乘方;再乘除;最后算加减。7.有括号,先算括号内的运算,按小括号、中括号、大括号依次进行。8.同级运算,从左到右进行。知识点九近似数1.近似数:在一定程度上反映被考察量的大小,能说明实际问题的意义,与准确数非常地接近,像这样的数我们称它为近似数。2.近似数的分类(1)具体近似数(如30.2、58.0⋯)(2)带单位近似数(如2.4万⋯)(3)科学记数法3.精确度:用位数较少的近似数替代位数较多或位数无限的数,有一个近似程度的问题,这个近似程度就是精确度。四舍五入到哪一位,就说精确到哪一位(看精确度得到原数中去看在哪一位上,如:2.4万精确到千位,而非十分位,因为2.4万就是24000,4在千位上)。4.有效数字:对于一个不为0的近似数,从左边第一个不为0的数字起,到末尾数止,所有数字都是这个近似数的有效数字。求近似数要求保留n个有效数字时,第n+1个有效数字作四舍五入处理。例:0.0109有三个有效数字1、0、9,要求保留2个有效数字时,0.0109的第三个有效数字9四舍五入,变为0.0110,保留两个有效数字1、1后求出近似数0.0109≈0.011。第二章整式的加减知识点一整式的相关概念代数式中的一种有理式:不含除法运算或分数,以及虽有除法运算及分数,但除式或分母中不含变数者,则称为整式。(分母中含有字母有除法运算的,那么式子叫做分式)1.单项式:数或字母的积(如5n),单个的数或字母也是单项式。学习必备...